Sách bài tập Toán 12 Bài 6 (Kết nối tri thức): Vectơ trong không gian

Giải SBT Toán 12 Bài 6: Vectơ trong không gian

Bài 2.1 trang 43 SBT Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Trong các vectơ có điểm đầu và điểm cuối phân biệt thuộc tập {S, A, B, C, D}:

a) Những vectơ nào có điểm đầu là S?

b) Những vectơ nào có giá nằm trong mặt phẳng (SAB)?

c) Vectơ nào là vectơ đối của vectơ $\overrightarrow{\mathrm{BC}}$?

Lời giải:

a) Những vectơ có điểm đầu là S là: $\overrightarrow{SA}$, $\overrightarrow{SB}$, $\overrightarrow{SC}$, $\overrightarrow{SD}$.

b) Những vectơ có giá nằm trong mặt phẳng (SAB) là: $\overrightarrow{SA}$, $\overrightarrow{SB}$, $\overrightarrow{BS}$, $\overrightarrow{AS}$, $\overrightarrow{AB}$, $\overrightarrow{BA}$.

c) Vectơ đối của vectơ $\overrightarrow{BC}$ là: $\overrightarrow{CB}$.

Bài 2.2 trang 44 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Trong các vectơ có điểm đầu và điểm cuối là hai đỉnh phân biệt của hình hộp:

a) Vectơ nào cùng phương với vectơ $\overrightarrow{AC}$?

b) Vectơ nào bằng vectơ $\overrightarrow{A{D}^{‘}}$?

c) Những vectơ nào là vectơ đối của vectơ $\overrightarrow{A{A}^{‘}}$?

Lời giải:

a) Ta có tứ giác ACC’A’ là hình bình hành nên AC // A’C’, suy ra $\overrightarrow{A^{‘}{C}^{‘}}$ cùng phương với vectơ $\overrightarrow{AC}$.

Do đó, các vec tơ $\overrightarrow{CA}$, $\overrightarrow{A^{‘}{C}^{‘}}$ và $\overrightarrow{C^{‘}{A}^{‘}}$ cũng cùng phương với $\overrightarrow{AC}$.

Vectơ cùng phương với vectơ $\overrightarrow{AC}$ là: $\overrightarrow{CA}$, $\overrightarrow{A^{‘}{C}^{‘}}$ và $\overrightarrow{C^{‘}{A}^{‘}}$.

b) Tứ giác ABC’D’ là hình bình hành nên $\overrightarrow{A{D}^{‘}}=\overrightarrow{B{C}^{‘}}$.

c) Vectơ đối của vectơ $\overrightarrow{A{A}^{‘}}$ là: $\overrightarrow{A^{‘}A}$, $\overrightarrow{B^{‘}B}$, $\overrightarrow{C^{‘}C}$, $\overrightarrow{D^{‘}D}$.

Bài 2.3 trang 44 SBT Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AD = 1 và AA’ = 2. Tính độ dài của các vectơ sau:

a) $\overrightarrow{\mathrm{BD}}$;

b) $\overrightarrow{{\mathrm{CD}}^{‘}}$;

c) $\overrightarrow{{\mathrm{AC}}^{‘}}$.

Lời giải:

a) Ta có tam giác ABD vuông tại cân tại A và AB = AD = 1,

Suy ra $\left|\overrightarrow{\mathrm{BD}}\right|$ = BD = $\sqrt{A{B}^2+A{D}^2}$= $\sqrt{2}$.

b) Tam giác CDD’ vuông tại D có CD = AB = 1, DD’ = AA’ = 2.

Do đó, $\left|\overrightarrow{{\mathrm{CD}}^{‘}}\right|$ = CD’ = $\sqrt{5}$.

c) Do AB = AD = 1 nên đáy ABCD là hình vuông, suy ra AC = BD = $\sqrt{2}$.

Tam giác ACC’ vuông tại C, có AC = $\sqrt{2}$ và CC’ = 2.

Suy ra $\left|\overrightarrow{A{C}^{‘}}\right|$ = AC’ = $\sqrt{C{C^{‘}}^2+A{C}^2}$ = $\sqrt{6}$.

Bài 2.4 trang 44 SBT Toán 12 Tập 1: Trong không gian, cho năm điểm phân biệt A, B, C, D, E. Chứng minh rằng:

a) $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AE}-\overrightarrow{DE}$;

b) $\overrightarrow{AB}+\overrightarrow{DE}=\overrightarrow{AE}-\overrightarrow{BD}$;

c) $\overrightarrow{BC}+\overrightarrow{DE}=\overrightarrow{BE}-\overrightarrow{CD}$.

Lời giải:

a) Ta có: $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=$$\overrightarrow{AC}$ + $\overrightarrow{CD}$ = $\overrightarrow{AD}$ = $\overrightarrow{AE}+\overrightarrow{ED}$ = $\overrightarrow{AE}-\overrightarrow{DE}$.

Vậy $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AE}-\overrightarrow{DE}$.

b) Ta có: $\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}=\overrightarrow{AE}+\overrightarrow{ED}$

          ⇒ $\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AE}+\overrightarrow{ED}$

        ⇔  $\overrightarrow{AB}-\overrightarrow{ED}=\overrightarrow{AE}-\overrightarrow{BD}$

         ⇔ $\overrightarrow{AB}+\overrightarrow{DE}=\overrightarrow{AE}-\overrightarrow{BD}$

Vậy ta có đpcm.

c) Ta có: $\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{BD}=\overrightarrow{BE}+\overrightarrow{ED}$

          ⇒ $\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{BE}+\overrightarrow{ED}$

          ⇔ $\overrightarrow{BC}-\overrightarrow{ED}=\overrightarrow{BE}-\overrightarrow{CD}$

          ⇔ $\overrightarrow{BC}+\overrightarrow{DE}=\overrightarrow{BE}-\overrightarrow{CD}$

Vậy ta có đpcm.

Bài 2.5 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc các cạnh AB, CD sao cho AE = $\frac{1}{3}$AB và CF = $\frac{1}{3}$CD. Chứng minh rằng:

a) $\overrightarrow{EF}=\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$;

b) $\overrightarrow{EF}=\overrightarrow{BC}+\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{CD}$;

c) $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BC}+\frac{1}{3}\overrightarrow{AB}$.

Lời giải:

a) Ta có: $\overrightarrow{EF}=\overrightarrow{EA}+\overrightarrow{AD}+\overrightarrow{DF}$

                     = $–\overrightarrow{AE}+\overrightarrow{AD}–\overrightarrow{FD}$

                     = $\overrightarrow{AD}–\frac{1}{3}\overrightarrow{AB}–\frac{2}{3}\overrightarrow{CD}$.

Vậy $\overrightarrow{EF}=\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$.

b) Ta có: $\overrightarrow{EF}=\overrightarrow{EB}+\overrightarrow{BC}+\overrightarrow{CF}$

                     = $\frac{2}{3}\overrightarrow{AB}+\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CD}$.

Vậy $\overrightarrow{EF}=\overrightarrow{BC}+\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{CD}$.

c) Từ câu a và b, ta có:

$3\overrightarrow{EF}=\left(\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}\right)+2\left(\frac{2}{3}\overrightarrow{AB}+\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CD}\right)$

        = $\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$

        = $\overrightarrow{AD}$ + $\overrightarrow{AD}-\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{CD}$ + $\left(-\frac{2}{3}\overrightarrow{CD}+\frac{2}{3}\overrightarrow{CD}\right)$ + $2\overrightarrow{CB}$

        = $\overrightarrow{AD}+2\overrightarrow{CB}+\overrightarrow{AB}$

⇒ $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BC}+\frac{1}{3}\overrightarrow{AB}$.

Vậy ta có đpcm.

Bài 2.6 trang 44 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, BD. Gọi E, F lần lượt là trọng tâm của các tam giác ABC, ABD. Chứng minh rằng:

a) $\overrightarrow{EF}=\frac{2}{3}\overrightarrow{MN}$;

b) $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{CD}$.

Lời giải:

a) Xét tam giác AMN, ta có: AE = $\frac{2}{3}$AM, AF = $\frac{2}{3}$AN (E, F là trọng tâm tam giác ABC, ABD).

Theo định lí Thales đảo suy EF // MN và EF = $\frac{2}{3}$MN.

Vì $\overrightarrow{EF}$ và $\overrightarrow{MN}$ cùng hướng nên $\overrightarrow{EF}=\frac{2}{3}\overrightarrow{MN}$.

b) Xét tam giác BCD, có M, N là trung điểm CB, DB nên MN là đường trung bình của tam giác.

Ta có: MN // CD và MN = $\frac{1}{2}$CD.

$\overrightarrow{CD}$ và $\overrightarrow{MN}$ cùng hướng nên $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{CD}$.

Do đó, $\overrightarrow{EF}=\frac{2}{3}\overrightarrow{MN}=\frac{2}{3}.\frac{1}{2}\overrightarrow{CD}=\frac{1}{3}\overrightarrow{CD}$.

Vậy $\overrightarrow{EF}=\frac{1}{3}\overrightarrow{CD}$.

Bài 2.7 trang 44 SBT Toán 12 Tập 1: Một tòa chung cư có chiều cao của các tầng như nhau. Một thang máy di chuyển từ tầng 10 lên tầng 26 của tòa nhà, sau đó di chuyển từ tầng 26 xuống tầng 18. Hãy cho biết mối liên hệ về phương, hướng, độ dài của các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó, từ đó phát biểu một đẳng thức liên hệ giữa hai vectơ đó.

Lời giải:

Gọi vectơ thể hiện độ dịch chuyển của thang máy từ tầng 10 lên tầng 26 là $\overrightarrow{a}$.

Gọi vectơ thể hiện độ dịch chuyển của thang máy từ tầng 26 xuống tầng 18 là $\overrightarrow{b}$.

Khi đó, $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương và ngược hướng.

Hơn nữa độ dài của $\overrightarrow{a}$ bằng độ cao của 16 tầng, độ dài của $\overrightarrow{b}$ bằng độ cao của 8 tầng, suy ra $\left|\overrightarrow{a}\right|=2\left|\overrightarrow{b}\right|$.

Từ cách lập luận trên suy ra $\overrightarrow{a}=\left(-2\right)\overrightarrow{b}=-2\overrightarrow{b}$.

Bài 2.8 trang 45 SBT Toán 12 Tập 1: Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và ba chân bàn vuông góc với mặt sàn. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ $\overrightarrow{u}$) phân tán đều qua các chân bàn và tạo nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$). Hãy giải thích vì sao $\overrightarrow{x}=\overrightarrow{y}=\overrightarrow{z}=-\frac{1}{3}\overrightarrow{u}$.

Lời giải:

Các vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ đôi một cùng phương vì giá của chúng đề vuông góc với mặt đất. Ba vectơ đó cùng hướng vì đều ngược hướng với trọng lực.

Ba vectơ đó có độ lớn bằng nhau vì trọng lực phân tán đều qua ba chân bàn.

Do đó $\overrightarrow{x}=\overrightarrow{y}=\overrightarrow{z}$.

Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{u}$ cùng phương, ngược hướng và $\left|\overrightarrow{x}\right|=\frac{1}{3}\left|\overrightarrow{u}\right|$ nên $\overrightarrow{x}=-\frac{1}{3}\overrightarrow{u}$.

Vậy $\overrightarrow{x}=\overrightarrow{y}=\overrightarrow{z}=-\frac{1}{3}\overrightarrow{u}$.

Bài 2.9 trang 45 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Đặt $\overrightarrow{A{A}^{‘}}=\overrightarrow{x}$, $\overrightarrow{AB}=\overrightarrow{y}$ và $\overrightarrow{AC}=\overrightarrow{z}$. Hãy biểu diễn các vectơ sau qua ba vectơ $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$:

a) $\overrightarrow{AD}$;

b) $\overrightarrow{A{C}^{‘}}$;

c) $\overrightarrow{B{D}^{‘}}$.

Lời giải:

a) Ta có: $\overrightarrow{AD}=\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{z}-\overrightarrow{y}$.

b) Ta có:

$\overrightarrow{A{C}^{‘}}=\overrightarrow{A{A}^{‘}}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{x}+\overrightarrow{y}+\left(\overrightarrow{z}-\overrightarrow{y}\right)=\overrightarrow{x}+\overrightarrow{z}$.

c) Ta có: $\overrightarrow{B{D}^{‘}}$ = $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{B{B}^{‘}}$ = $-\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{‘}}$

                     = −$\overrightarrow{y}+\left(\overrightarrow{z}-\overrightarrow{y}\right)+\overrightarrow{x}$ = $\overrightarrow{x}-2\overrightarrow{y}+\overrightarrow{z}$.

Bài 2.10 trang 45 SBT Toán 12 Tập 1: Trong không gian, cho hai hình bình hành ABCD và A’B’C’D’. Chứng minh rằng:

a) $\overrightarrow{B{B}^{‘}}+\overrightarrow{D{D}^{‘}}=\overrightarrow{A{B}^{‘}}+\overrightarrow{A{D}^{‘}}-\overrightarrow{AB}-\overrightarrow{AD}$;

b) $\overrightarrow{B{B}^{‘}}+\overrightarrow{D{D}^{‘}}=\overrightarrow{C{C}^{‘}}$.

Lời giải:

a) Ta có: $\overrightarrow{B{B}^{‘}}=\overrightarrow{A{B}^{‘}}-\overrightarrow{AB}$ và $\overrightarrow{D{D}^{‘}}=\overrightarrow{A{D}^{‘}}-\overrightarrow{AD}$.

Suy ra $\overrightarrow{B{B}^{‘}}+\overrightarrow{D{D}^{‘}}=\overrightarrow{A{B}^{‘}}+\overrightarrow{A{D}^{‘}}-\overrightarrow{AB}-\overrightarrow{AD}$.

b) Vì tứ giác ABCD là hình bình hành nên $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

Vì tứ giác A’B’C’D’ là hình bình hành nên $\overrightarrow{A{B}^{‘}}+\overrightarrow{A{D}^{‘}}=\overrightarrow{A{C}^{‘}}$.

Kết hợp với câu a suy ra

$\overrightarrow{B{B}^{‘}}+\overrightarrow{D{D}^{‘}}=\overrightarrow{A{B}^{‘}}+\overrightarrow{A{D}^{‘}}-\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{A{C}^{‘}}-\overrightarrow{AC}$.

Bài 2.11 trang 45 SBT Toán 12 Tập 1: Cho hình lăng trụ đứng ABCD.A’B’C’D’. Biết rằng AA’ = 2 và tứ giác ABCD là hình thoi có AB = 1 và $\widehat{ABC}$ = 60°, hãy tính góc giữa các cặp vectơ sau và từ đó tính tích vô hướng của mỗi cặp vectơ đó:

a) $\overrightarrow{AB}$ và $\overrightarrow{A^{‘}{D}^{‘}}$;

b) $\overrightarrow{A{A}^{‘}}$ và $\overrightarrow{BD}$;

c) $\overrightarrow{AB}$ và $\overrightarrow{A^{‘}{C}^{‘}}$.

Lời giải:

a) Ta có:

$\left(\overrightarrow{AB},\overrightarrow{A^{‘}{D}^{‘}}\right)=\left(\overrightarrow{AB},\overrightarrow{AD}\right)=\widehat{BAC}=180°-60°=120°$.

Do đó, $\overrightarrow{AB}.\overrightarrow{A^{‘}{D}^{‘}}=AB.A^{‘}{D}^{‘}.\cos \left(\overrightarrow{AB},\overrightarrow{A^{‘}{D}^{‘}}\right)$ = 1.1. cos120° = $-\frac{1}{2}$

b) Ta có: AA’ vuông góc với mặt phẳng (ABCD) nên $\left(\overrightarrow{A{A}^{‘}},\overrightarrow{BD}\right)$ = 90°.

Do đó,$\overrightarrow{A{A}^{‘}}.\overrightarrow{BD}$ = AA’.BD.cos90° = 0.

c) Tam giác ABC có AB = BC = 1 và $\widehat{ABC}$ = 60° nên tam giác ABC đều.

Do đó, $\widehat{BAC}$ = 60° và AC = 1.

Ta có: $\left(\overrightarrow{AB},\overrightarrow{A^{‘}{C}^{‘}}\right)=\left(\overrightarrow{AB},\overrightarrow{AC}\right)=\widehat{BAC}$ = 60° và $\overrightarrow{AB}.\overrightarrow{A^{‘}{C}^{‘}}$ = AB.A’C’.cos60° = 1.1.$\frac{1}{2}$ = $\frac{1}{2}$.

Bài 2.12 trang 46 SBT Toán 12 Tập 1: Trong không gian, cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ thỏa mãn $\left|\overrightarrow{a}\right|$ = 1, $\left|\overrightarrow{b}\right|$ = 2 và $\left(\overrightarrow{a},\overrightarrow{b}\right)$ = 45°. Tính các tích vô hướng sau:

a) ${\left(\overrightarrow{a}+\overrightarrow{b}\right)}^2$;

b) $\left(\overrightarrow{a}+\overrightarrow{b}\right).\left(\overrightarrow{a}-\overrightarrow{b}\right)$;

c) $\left(2\overrightarrow{a}-\overrightarrow{b}\right).\left(\overrightarrow{a}+3\overrightarrow{b}\right)$.

Lời giải:

a) Ta có: ${\left(\overrightarrow{a}+\overrightarrow{b}\right)}^2$ = ${\overrightarrow{a}}^2+2\overrightarrow{a}\overrightarrow{b}+{\overrightarrow{b}}^2$= 1² + 2² + 2.1.2.cos45° = 5 + 2$\sqrt{2}$.

b) Ta có: $\left(\overrightarrow{a}+\overrightarrow{b}\right).\left(\overrightarrow{a}-\overrightarrow{b}\right)$= ${\overrightarrow{a}}^2-{\overrightarrow{b}}^2$ = 1² – 2² = −3.

c) Ta có: $\left(2\overrightarrow{a}-\overrightarrow{b}\right).\left(\overrightarrow{a}+3\overrightarrow{b}\right)$ = $2{\overrightarrow{a}}^2-3{\overrightarrow{b}}^2+5\overrightarrow{a}.\overrightarrow{b}$ = 2.1² – 3.2² + 5.1.2.cos45° = −10 + 5$\sqrt{2}$.

Bài 2.13 trang 46 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi G là giao điểm của MP và NQ. Chứng minh rằng $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}.$

Lời giải:

Vì MN là đường trung bình của tam giác ABC nên MN // AC và MN = $\frac{1}{2}$AC.

Vì PQ là đường trung bình của tam giác ADC nên NP // AC và NP = $\frac{1}{2}$AC.

Do dó, MN //AC và MNPQ là hình bình hành.

Theo đề bài, G là giao điểm của MNPQ là hình bình hành và G là giao điểm MP và NQ nên G là trung điểm của mỗi đoạn thẳng đó.

Ta có: $\left(\overrightarrow{GA}+\overrightarrow{GB}\right)+\left(\overrightarrow{GC}+\overrightarrow{GD}\right)$ = $2\overrightarrow{GM}+2\overrightarrow{GP}$ = 2$\left(\overrightarrow{GM}+\overrightarrow{GP}\right)$ = 2.$\overrightarrow{0}$ = $\overrightarrow{0}$.

Bài 2.14 trang 46 SBT Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’ có độ dài các cạnh bằng a. Tính các tích vô hướng sau theo a:

a) $\overrightarrow{AC}.\overrightarrow{B^{‘}{D}^{‘}}$;

b) $\overrightarrow{BD}.\overrightarrow{B^{‘}{C}^{‘}}$;

c) $\overrightarrow{A^{‘}{B}^{‘}}.\overrightarrow{A{C}^{‘}}$.

Lời giải:

a) Do hai vectơ $\overrightarrow{AC}$ và $\overrightarrow{B^{‘}{D}^{‘}}$ vuông góc với nhau nên $\overrightarrow{AC}.\overrightarrow{B^{‘}{D}^{‘}}$ = 0

b) Ta có: $\overrightarrow{BD}.\overrightarrow{B^{‘}{C}^{‘}}$ = $\overrightarrow{BD}.\overrightarrow{BC}$ = BD.BD.cos45° = a.a$\sqrt{2}$.cos45° = a².

c) Ta có: $\overrightarrow{A^{‘}{B}^{‘}}.\overrightarrow{A{C}^{‘}}$ = $\overrightarrow{AB}.\overrightarrow{A{C}^{‘}}$

                             = $\overrightarrow{AB}.\left(\overrightarrow{A{A}^{‘}}+\overrightarrow{AC}\right)$

                             = $\overrightarrow{AB}.\overrightarrow{A{A}^{‘}}+\overrightarrow{AB}.\overrightarrow{AC}$

                             = 0 + AB.AC.cos45° = a.a$\sqrt{2}$.$\frac{\sqrt{2}}{2}$ = a².

Bài 2.15 trang 46 SBT Toán 12 Tập 1: Cho hình chóp S.ABC có SA = SB = SC và $\widehat{ASB}=\widehat{BSC}=\widehat{CSA}$. Chứng minh rằng $\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SC}.\overrightarrow{AB}=0$.

Lời giải:

Ta có: $\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}\left(\overrightarrow{SC}-\overrightarrow{SB}\right)$

                             = $\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}$

                              = SA.SC.cos$\widehat{ASC}$ − SA.SB.cos$\widehat{ASB}$

                             = 0.

          $\overrightarrow{SB}.\overrightarrow{AC}$ = $\overrightarrow{SB}\left(\overrightarrow{SC}-\overrightarrow{SA}\right)$

                             = $\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}$

                             = SC.SB.cos$\widehat{BSC}$ − SA.SB.cos$\widehat{ASB}$

                             = 0.

          $\overrightarrow{SC}.\overrightarrow{AB}$ = $\overrightarrow{SC}\left(\overrightarrow{SB}-\overrightarrow{SA}\right)$

                             = $\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SC}$

                             = SC.SB.cos$\widehat{BSC}$ − SA.SC.cos$\widehat{ASC}$

                             = 0.

Vậy $\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SC}.\overrightarrow{AB}=0$.

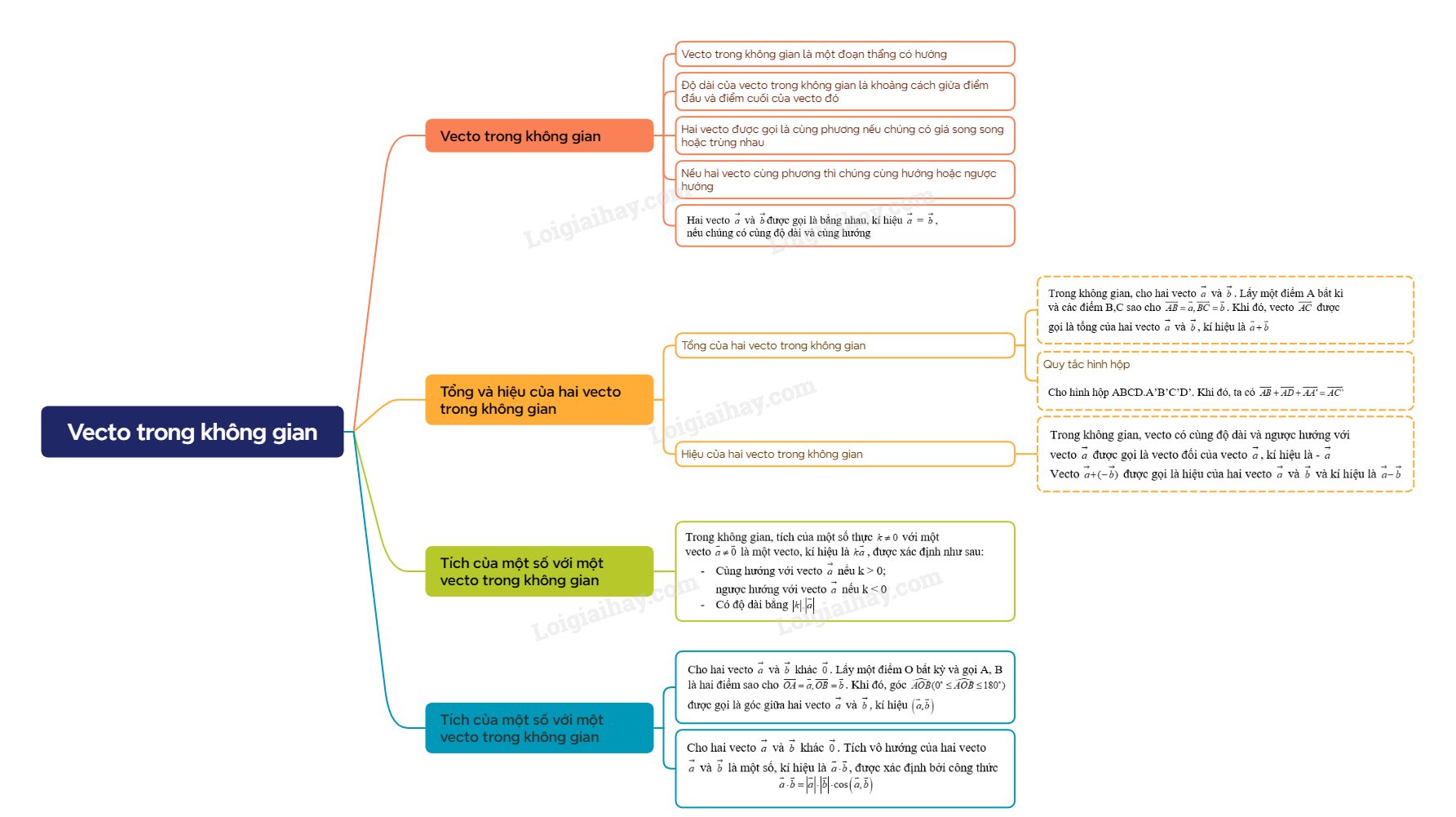
Lý thuyết Vectơ trong không gian

1. Vecto trong không gian

Khái niệm vecto trong không gian

– Vecto trong không gian là một đoạn thẳng có hướng – Độ dài của vecto trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vecto đó – Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau – Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng – Hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$được gọi là bằng nhau, kí hiệu $\overrightarrow{a}$ = $\overrightarrow{b}$, nếu chúng có cùng độ dài và cùng hướng

2. Tổng và hiệu của hai vecto trong không gian

a) Tổng của hai vecto trong không gian

Trong không gian, cho hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$. Lấy một điểm A bất kì và các điểm B,C sao cho $\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{BC}=\overrightarrow{b}$. Khi đó, vecto $\overrightarrow{AC}$ được gọi là tổng của hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu là $\overrightarrow{a}+\overrightarrow{b}$ Trong không gian, phép lấy tổng của hai vecto được gọi là phép cộng vecto

 Quy tắc hình hộp

Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\prime }}=\overrightarrow{A{C}^{\prime }}$

 b) Hiệu của hai vecto trong không gian

Trong không gian, vecto có cùng độ dài và ngược hướng với vecto $\overrightarrow{a}$ được gọi là vecto đối của vecto $\overrightarrow{a}$, kí hiệu là – $\overrightarrow{a}$ Vecto $\overrightarrow{a}+(-\overrightarrow{b})$ được gọi là hiệu của hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ và kí hiệu là $\overrightarrow{a}-\overrightarrow{b}$ Trong không gian, phép lấy hiệu của hai vecto được gọi là phép trừ vecto

3. Tích của một số với một vecto trong không gian

Trong không gian, tích của một số thực $k\ne 0$ với một vecto $\overrightarrow{a}\ne \overrightarrow{0}$ là một vecto, kí hiệu là $k\overrightarrow{a}$, được xác định như sau: – Cùng hướng với vecto $\overrightarrow{a}$ nếu k > 0; ngược hướng với vecto $\overrightarrow{a}$ nếu k < 0 – Có độ dài bằng $\left|k\right|.\left|\overrightarrow{a}\right|$ Trong không gian, phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto

4. Tích vô hướng của hai vecto trong không gian

a) Góc giữa hai vecto trong không gian

Trong không gian, cho hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ khác $\overrightarrow{0}$. Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho $\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$. Khi đó, góc $\widehat{AOB}(0^{\circ }\le \widehat{AOB}\le {180}^{\circ })$ được gọi là góc giữa hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu $\left(\overrightarrow{a},\overrightarrow{b}\right)$

b) Tích vô hướng của hai vecto trong không gian

Trong không gian, cho hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ khác $\overrightarrow{0}$. Tích vô hướng của hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ là một số, kí hiệu là $\overrightarrow{a}\cdot \overrightarrow{b}$, được xác định bởi công thức $\overrightarrow{a}\cdot \overrightarrow{b}=\left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{b}\right|\cdot \cos \left(\overrightarrow{a},\overrightarrow{b}\right)$

Sơ đồ tư duy Vectơ trong không gian

Xem thêm các bài giải SBT Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 1

Bài 6: Vectơ trong không gian

Bài 7: Hệ trục toạ độ trong không gian

Bài 8: Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2

Bài 9: Khoảng biến thiên và khoảng tứ phân vị