Sách bài tập Toán 12 Bài 8 (Kết nối tri thức): Biểu thức toạ độ của các phép toán vectơ

Giải SBT Toán 12 Bài 8: Biểu thức toạ độ của các phép toán vectơ

Bài 2.25 trang 54 SBT Toán 12 Tập 1: Trong không gian Oxyz, cho ba vectơ $\overrightarrow{a}$ = (3; 0; 4), $\overrightarrow{b}$ = (2; 7; 7) và $\overrightarrow{c}$ = (2; 7; 2).

a) Tìm tọa độ của các vectơ $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ và $2\overrightarrow{a}+3\overrightarrow{b}-4\overrightarrow{c}$.

b) Tính các tích vô hướng $\left(-\overrightarrow{a}\right).\overrightarrow{b}$ và $\left(3\overrightarrow{a}\right)$.$\overrightarrow{c}$.

c) Tính côsin của các góc $\left(\overrightarrow{a},\overrightarrow{b}\right)$ và $\left(\overrightarrow{a},\overrightarrow{c}\right)$.

Lời giải:

a) Ta có: $\overrightarrow{a}-\overrightarrow{b}$ = (3 – 2;0 – 7;4 – 7) = (1; −7; −3).

Do đó, $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ = (1 + 2; −7 + 7; −3 + 2) = (3; 0; −1).

Vậy $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ = (3; 0; −1).

Ta có: 2$\overrightarrow{a}$ = (6; 0; 8), $3\overrightarrow{b}$ = (6; 21; 21), $4\overrightarrow{c}$ = (8; 28; 8).

Do đó, $2\overrightarrow{a}+3\overrightarrow{b}-4\overrightarrow{c}$ = (4; −7; 21).

b) Ta có: −$\overrightarrow{a}$ = (−3; 0; −4).

Do đó, $\left(-\overrightarrow{a}\right).\overrightarrow{b}$ = −3.2 + 0.7 + (−4).7 = −34.

Ta có: 3$\overrightarrow{a}$ = (9; 0; 12).

Do đó, $\left(3\overrightarrow{a}\right)$.$\overrightarrow{c}$ = 9.2 + 0.7 + 12.2 = 42.

c) Ta có:

cos$\left(\overrightarrow{a},\overrightarrow{b}\right)$ = $\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}$ = $\frac{3.2+0.7+4.7}{\sqrt{3^2+0^2+4^2}.\sqrt{2^2+7^2+7^2}}$ = $\frac{\sqrt{102}}{15}$.

Ta có:

cos$\left(\overrightarrow{a},\overrightarrow{c}\right)$ = $\frac{\overrightarrow{a}.\overrightarrow{c}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{c}\right|}$ = $\frac{3.2+0.7+4.2}{\sqrt{3^2+0^2+4^2}.\sqrt{2^2+7^2+2^2}}$ = $\frac{14}{5\sqrt{57}}$.

Bài 2.26 trang 54 SBT Toán 12 Tập 1: Trong không gian Oxyz, cho hai vectơ $\overrightarrow{a}$ = (m; 3; 6) và $\overrightarrow{b}$ = (1; 2; 3). Xác định giá trị của m trong những trường hợp sau:

a) $\overrightarrow{a}-2\overrightarrow{b}$ = (3; −1; 0);

b) $\overrightarrow{a}.\overrightarrow{b}$ = 10;

c) $\left|\overrightarrow{a}\right|$ = 9.

Lời giải:

a) Ta có: $2\overrightarrow{b}$ = (2; 4; 6)

Suy ra $\overrightarrow{a}-2\overrightarrow{b}$ = (m – 2; 3 – 4; 6 – 6) = (m – 2; −1; 0).

Mà $\overrightarrow{a}-2\overrightarrow{b}$ = (3; −1; 0) = (m – 2; −1; 0).

Do đó, m – 2 = 3 hay m = 5.

b) Ta có: $\overrightarrow{a}.\overrightarrow{b}$ = m.1 + 3.2 + 6.3 = m + 24 = 10

Suy ra m = −14.

c) Ta có: $\left|\overrightarrow{a}\right|$ = $\sqrt{m^2+3^2+6^2}=9$

                   ⇒ $\sqrt{m^2+45}=9$

                   ⇒ m² + 45 = 81

                   ⇒ m² = 36

                   ⇒ m = ±6.

Bài 2.27 trang 54 SBT Toán 12 Tập 1: Trong không gian Oxyz, cho tứ diện ABCD với A(1; 3; −3), B(2; 0; 5), C(6; 9; −5) và D(−1; −4; 3).

a) Tìm tọa độ trọng tâm I của tam giác ABC.

b) Tìm tọa độ của điểm G thuộc đoạn thẳng DI sao cho DG = 3IG.

Lời giải:

a) Gọi I(x; y; z)

Ta có: I là trọng tâm tam giác ABC nên

$\left\{\begin{array}{l}x=\frac{1+2+6}{3}\\ y=\frac{3+0+9}{3}\\ z=\frac{-3+5+(-5)}{3}\end{array}\right.$ ⇔ $\left\{\begin{array}{l}x=3\\ y=4\\ z=-1\end{array}\right.$.

Vậy I(3; 4; −1).

b) Gọi G(x₀; y₀; z₀), theo đề ta có: DG = 3IG nên DG = $\frac{3}{4}$DI suy ra $\overrightarrow{DG}=\frac{3}{4}\overrightarrow{DI}$.

Suy ra $\left\{\begin{array}{l}{x}_0+1=\frac{3}{4}.4\\ y_0+4=\frac{3}{4}.8\\ z_0-3=\frac{3}{4}.(-4)\end{array}\right.$ ⇒ $\left\{\begin{array}{l}{x}_0=2\\ y_0=2\\ z_0=0\end{array}\right.$.

Vậy G(2; 2; 0).

Bài 2.28 trang 54 SBT Toán 12 Tập 1: Cho tứ diện ABCD. Trọng tâm G của tứ diện là điểm duy nhất thỏa mãn đẳng thức $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$. Chứng minh rằng tọa độ của điểm G được cho bởi công thức:

x_G = $\frac{x_A+x_B+x_C+x_D}{4}$;

y_G = $\frac{y_A+y_B+y_C+y_D}{4}$;

z_G= $\frac{z_A+z_B+z_C+z_D}{4}$.

Lời giải:

Ta có: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$

$\overrightarrow{OA}-\overrightarrow{OG}+\overrightarrow{OB}-\overrightarrow{OG}+\overrightarrow{OC}-\overrightarrow{OG}+\overrightarrow{OD}-\overrightarrow{OG}=\overrightarrow{0}$

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}-4\overrightarrow{OG}=\overrightarrow{0}$

$\frac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)=\overrightarrow{OG}$

Do đó, $\overrightarrow{OG}=\frac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)$.

Vậy từ đây, với biểu thức tọa độ của phép cộng vectơ và phép nhân một số với một vectơ ta được:

x_G = $\frac{x_A+x_B+x_C+x_D}{4}$;

y_G = $\frac{y_A+y_B+y_C+y_D}{4}$;

z_G= $\frac{z_A+z_B+z_C+z_D}{4}$.

Bài 2.29 trang 54 SBT Toán 12 Tập 1: Trong không gian Oxyz, cho tam giác ABC với A(3; 5; 2), B(0; 6; 2) và C(2; 3; 6). Hãy giải tam giác ABC.

Lời giải:

Ta có: AB = $\sqrt{{\left(0-3\right)}^2+{\left(6-5\right)}^2+{\left(2-2\right)}^2}$ = $\sqrt{10}$;

           AC = $\sqrt{{\left(3-2\right)}^2+{\left(5-3\right)}^2+{\left(2-6\right)}^2}$ = $\sqrt{21}$;

           BC = $\sqrt{{\left(0-2\right)}^2+{\left(6-3\right)}^2+{\left(2-6\right)}^2}$ = $\sqrt{29}$.

cos$\widehat{BAC}$ = cos$\left(\overrightarrow{AC},\overrightarrow{AB}\right)$ = $\frac{\overrightarrow{AC}.\overrightarrow{AB}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}$ = $\frac{-3.(-1)+1.(-2)+0.4}{\sqrt{10}.\sqrt{21}}$ = $\frac{1}{\sqrt{210}}$.

Suy ra $\widehat{BAC}$ ≈ 86°.

cos$\widehat{ABC}$ = cos$\left(\overrightarrow{BA},\overrightarrow{BC}\right)$ = $\frac{\overrightarrow{BC}.\overrightarrow{BA}}{\left|\overrightarrow{BA}\right|.\left|\overrightarrow{BC}\right|}$ = $\frac{3.2+(-1).(-3)+0.4}{\sqrt{10}.\sqrt{29}}$ = $\frac{9}{\sqrt{290}}$.

Suy ra $\widehat{ABC}$ ≈ 58°.

Từ đây, $\widehat{ACB}$ = 180° − 86° − 58° = 36°.

Bài 2.30 trang 54 SBT Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1. Xét hệ tọa độ Oxyz gắn với hình lập phương như hình vẽ bên.

a) Tìm tọa độ các đỉnh của hình lập phương.

b) Tìm tọa độ trọng tâm G của tam giác B’CD’.

c) Chứng minh rằng ba điểm O, G, A thẳng hàng.

Lời giải:

a) Ta có: C'(0; 0; 0), D'(0; 1; 0), B'(1; 0; 0); C(0; 0; 1); D(0; 1; 1).

Ta có: $\overrightarrow{C{C}^{‘}}=\overrightarrow{A{A}^{‘}}=\overrightarrow{B{B}^{‘}}=\overrightarrow{D{D}^{‘}}$ = (0; 0; −1).

Gọi B(x; y; z), ta có: $\left\{\begin{array}{l}1-x=0\\ 0-y=0\\ 0-z=-1\end{array}\right.$⇔ $\left\{\begin{array}{l}x=1\\ y=0\\ z=1\end{array}\right.$.

Vậy B(1; 0; 1).

Ta có: $\overrightarrow{AB}=\overrightarrow{DC}$ ⇒ A(1; 1; 1).

          $\overrightarrow{C{C}^{‘}}=\overrightarrow{A{A}^{‘}}$⇒ A’ (1; 1; 0).

b) Gọi G(x_G; y_G; z_G), ta có:

$\left\{\begin{array}{l}{x}_G=\frac{1+0+0}{3}=\frac{1}{3}\\ y_G=\frac{0+1+0}{3}=\frac{1}{3}\\ z_G=\frac{0+0+1}{3}=\frac{1}{3}\end{array}\right.$.

Vậy G$\left(\frac{1}{3};\frac{1}{3};\frac{1}{3}\right)$.

c) Ta có: $\overrightarrow{OG}=\left(\frac{1}{3};\frac{1}{3};\frac{1}{3}\right)$, $\overrightarrow{OA}=(1;1;1).$

Có $\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OA}$ nên ba điểm O, G, A thẳng hàng.

Bài 2.31 trang 55 SBT Toán 12 Tập 1: Trên sân thể dục thầy giáo dựng hai chiếc cột vuông góc với mặt sân, chiều cao của mỗi chiếc cột lần lượt là 3 m và 2 m. Xét hệ tọa độ Oxyz sao cho mặt phẳng (Oxy) trùng với mặt sân, trục Oz hướng thẳng đứng lên trời. Đơn vị trong hệ tọa độ Oxyz được lấy theo mét.

a) Biết rằng chân của hai cột đó có tọa độ lần lượt là (8; 5; 0) và (3; 2; 0), hãy tìm tọa độ điểm đầu của mỗi cột.

b) Thầy giáo dự định căng một sợi dây nối hai đầu của hai cột. Hỏi sợi dây cần có độ dài tối thiểu là khoảng bao nhiêu mét?

Lời giải:

a) Ta thấy đầu chiếc cột có độ cao 3 m có tọa độ là (8; 5; 3), đầu chiếc cột có độ cao 2 m có tọa độ là (3; 2; 2).

b) Khoảng cách giữa hai đầu sợi dây của chiếc cột là:

$\sqrt{{\left(8-3\right)}^2+{\left(5-2\right)}^2+{\left(3-2\right)}^2}$ ≈ 5,92 (m).

Vậy sợi dây cần có độ dài tối thiểu 5,92 m.

Bài 2.32 trang 55 SBT Toán 12 Tập 1: Hình bên mô tả hai bức tường gạch được xây vuông góc với nhau và cùng vuông góc với mặt đất. Một người thợ xây căng dây giữa hai bức tường. Đầu A của sợi dây nằm trên bức tường thứ nhất, cách bức tường thứ hai là 3 m và cách mặt đất là 1,2 m. Đầu B của sợi dây nằm trên bức tường thứ hai, cách bức tường thứ nhất là 1 m và cách mặt đất là 2 m.

a) Hãy lập một hệ trục tọa độ phù hợp và tìm tọa độ của hai đầu A, B trong hệ tọa độ đó.

b) Tính độ dài của sợi dây được căng.

Lời giải:

a) Chọn hệ trục Oxyz như hình bên.

Khi đó tọa độ của hai đầu dây A, B là A(3; 0; 1,2) và B(0; 1; 2).

b) Độ dài của sợi dây là:

AB = $\sqrt{{\left(0-3\right)}^2+\left(1-0\right){+}_2{\left(2-1,2\right)}^2}$ ≈ 3,26 (m).

Lý thuyết Biểu thức toạ độ của các phép toán vectơ

1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto

Các phép toán vecto cơ bản

Trong không gian Oxyz, cho hai vecto $\overrightarrow{a}=(x;y;z)$ và $\overrightarrow{b}=(x^{\prime };y^{\prime };z^{\prime })$. Ta có: $\overrightarrow{a}+\overrightarrow{b}=(x+x^{\prime };y+y^{\prime };z+z^{\prime })$ $\overrightarrow{a}-\overrightarrow{b}=(x-x^{\prime };y-y^{\prime };z-z^{\prime })$ $k\overrightarrow{a}=(kx;ky;kz)$ với k là một số thực

 Công thức tính tọa độ trung điểm đoạn thẳng và trọng tâm tam giác

Trong không gian Oxyz, cho ba điểm không thẳng hàng$$A(x_A;y_A;z_A),B(x_B;y_B;z_B),C(x_C;y_C;z_C)$$. Khi đó: Tọa độ trung điểm của đoạn thẳng AB là$$\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2};\frac{z_A+z_B}{2}\right)$$ Tọa độ trọng tâm tam giác ABC là$$\left(\frac{x_A+x_B+x_C}{2};\frac{y_A+y_B+y_C}{2};\frac{z_A+z_B+z_C}{2}\right)$$

 2. Biểu thức tọa độ của tích vô hướng

Trong không gian Oxyz, tích vô hướng của hai vecto $\overrightarrow{a}=(x;y;z)$ và $\overrightarrow{b}=(x^{\prime };y^{\prime };z^{\prime })$ được xác định bởi công thức $\overrightarrow{a}\cdot \overrightarrow{b}=x{x}^{\prime }+y{y}^{\prime }+z{z}^{\prime }$

 3. Vận dụng tọa độ của vecto trong một số bài toán có liên quan đến thực tiễn

Ví dụ: Trong không gian với một hệ trục cho trước (đơn vị đo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B (940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 5 phút tiếp theo là gì?

Giải

Gọi C(x;y;z) là vị trí của máy bay sau 5 phút tiếp theo. Vì hướng của máy bay không đổi nên $\overrightarrow{AB}$ và $\overrightarrow{BC}$ cùng hướng. Do vận tốc bay không đổi và thời gian bay từ A đến B gấp đôi thời gian bay từ B đến C nên AB = 2 BC

Do đó,$$\overrightarrow{BC}=\frac{1}{2}\overrightarrow{AB}=\left(\frac{940-800}{2};\frac{550-500}{2};\frac{8-7}{2}\right)=\left(70;25;0,5\right)$$

Mặt khác,  nên $\{\begin{array}{l}x-940=70\\ y-550=25\\ z-8=0,5\end{array}$

Từ đó $\{\begin{array}{l}x=1010\\ y=575\\ z=8,5\end{array}$ và vì vậy C(1010;575;8,5)

Vậy tọa độ của máy bay sau 5 phút tiếp theo là (1010;575;8,5)

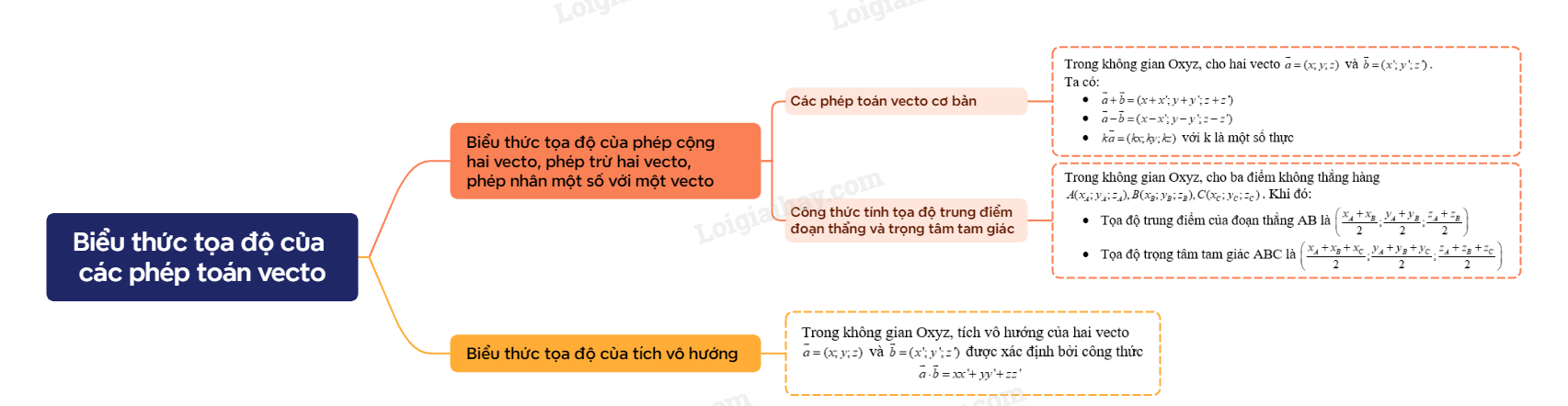
Sơ đồ tư duy Biểu thức toạ độ của các phép toán vectơ

Xem thêm các bài giải SBT Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 7: Hệ trục toạ độ trong không gian

Bài 8: Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2

Bài 9: Khoảng biến thiên và khoảng tứ phân vị

Bài 10: Phương sai và độ lệch chuẩn

Bài tập cuối chương 3