Giải bài tập Toán 12 Bài 1: Tính đơn điệu của hàm số
Hoạt động 1 trang 5 Toán 12 Tập 1: a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số có đồ thị như Hình 2.
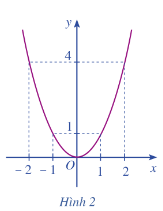
– Xác định khoảng đồng biến, nghịch biến của hàm số đó.
– Xét dấu đạo hàm .
– Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số và dấu của đạo hàm trên mỗi khoảng .
– Hoàn thành bảng biến thiên sau:
Lời giải:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và là hàm số xác định trên K.
– Hàm số được gọi là hàm số đồng biến trên K nếu với mọi thuộc K và thì .
– Hàm số được gọi là hàm số đồng biến trên K nếu với mọi thuộc K và thì .
– Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
– Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
– Đạo hàm âm khi và dương khi .
– Hàm số nghịch biến khi mang dấu âm và đồng biến khi mang dấu dương.
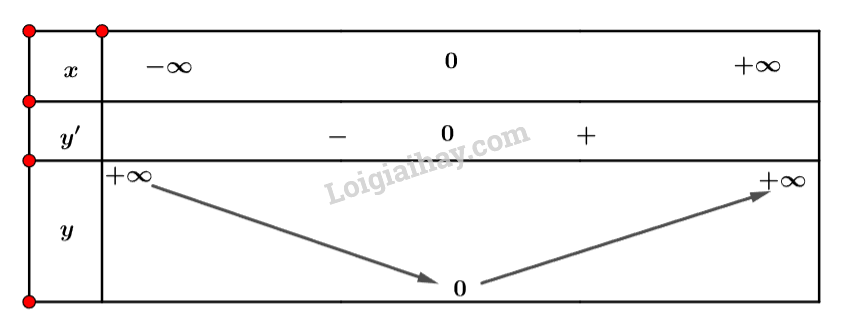
– Ta có bàng biến thiên sau:
Luyện tập 1 trang 6 Toán 12 Tập 1: Xét dấu rồi tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
Tập xác định .
Ta có: .
Xét .

Vậy hàm số đồng biến trên .
Luyện tập 2 trang 7 Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số .
Lời giải:
Tập xác định .
Ta có: .
Xét .
Ta có bảng biến thiên:
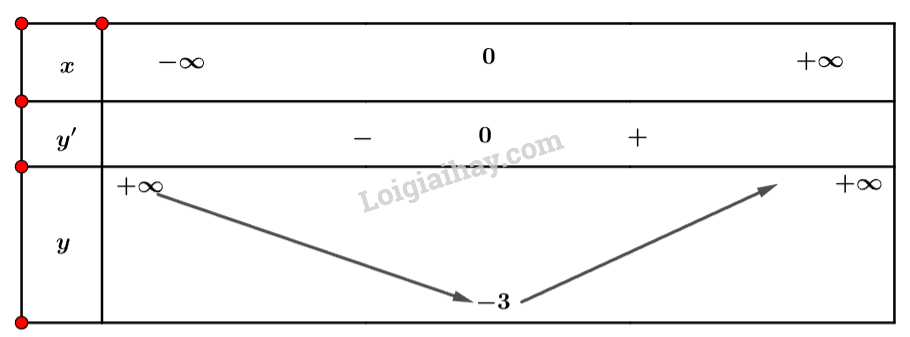
Vậy hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
Hoạt động 2 trang 7 Toán 12 Tập 1: a) Xác định tính đồng biến, nghịch biến của hàm số .
b) Xét dấu của đạo hàm .
c) Phương trình có bao nhiêu nghiệm ?
Lời giải:
a) Tập xác định .
Ta có: .
Xét .
Bảng biến thiên:
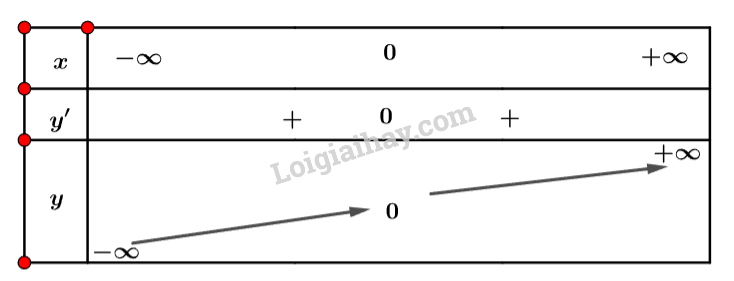
Vậy hàm số đồng biến trên .
b) Dựa vào bảng biến thiên ta thấy đạo hàm luôn dương với mọi x.
c) Phương trình có một nghiệm.
Luyện tập 3 trang 7 Toán 12 Tập 1: Chứng minh rằng hàm số nghịch biến trên nửa khoảng và đồng biến trên nửa khoảng .
Lời giải:
Tập xác định .
Ta có: .
Xét .
Ta có bảng biến thiên:
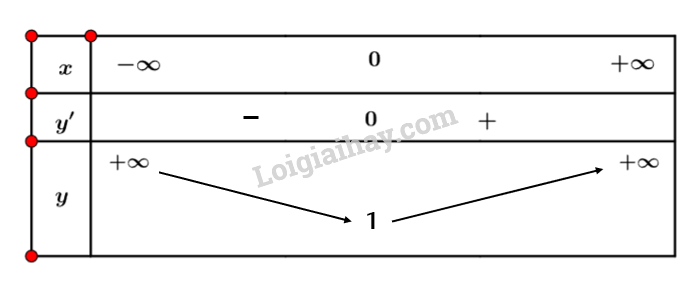
Vậy hàm số nghịch biến trên nửa khoảng và đồng biến trên nửa khoảng .
Luyện tập 4 trang 8 Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số sau .
Lời giải:
Tập xác định .
Ta có: .
Nhận xét: với mọi .
Ta có bảng biến thiên:
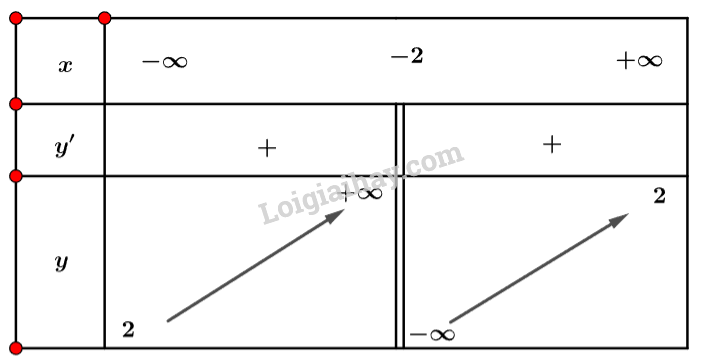
Vậy hàm số đồng biến trên mỗi khoảng và .
Hoạt động 3 trang 9 Toán 12 Tập 1: Dựa vào đồ thị hàm số ở Hình 3, hãy so sánh:
a) với mỗi giá trị , ở đó và .
b) với mỗi giá trị , ở đó và .
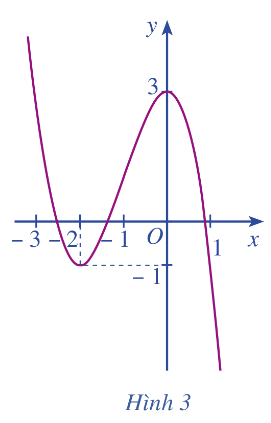
Lời giải:
a) Nhận xét: Ta thấy rằng với mọi và .
b) Tương tự: Ta thấy rằng với mọi và .
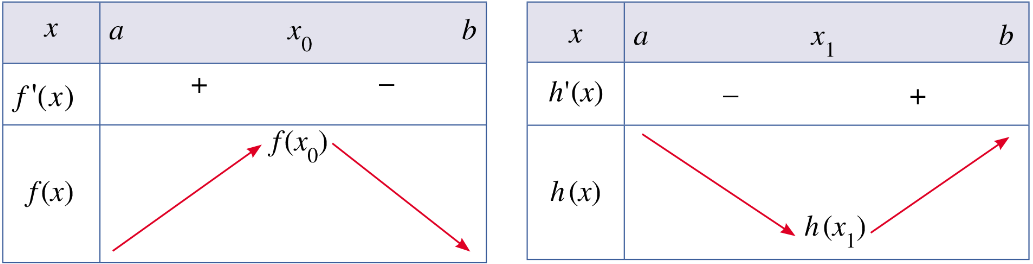
Hoạt động 4 trang 10 Toán 12 Tập 1: Quan sát bảng biến thiên dưới đây và cho biết:
a) có là điểm cực đại của hàm số hay không.
b) có là điểm cực tiểu của hàm số hay không.
Lời giải:
a) có là điểm cực đại của hàm số .
b) có là điểm cực tiểu của hàm số .
Luyện tập 5 trang 11 Toán 12 Tập 1: Tìm điểm cực trị của mỗi hàm số sau:
a) .
b) .
Lời giải:
a) Tập xác định: .
Ta có: .
Xét
Ta có bảng biến thiên sau:
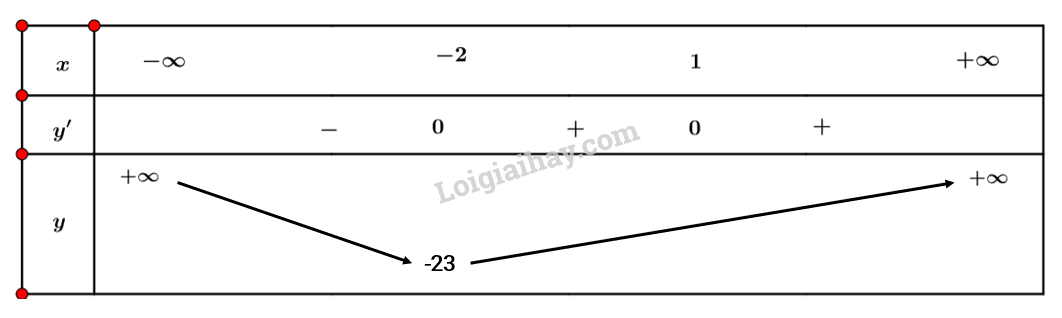
Vậy hàm số đạt cực đại tại điểm .
b) Tập xác định: .
Ta có: .
Nhận xét
Ta có bảng biến thiên sau:
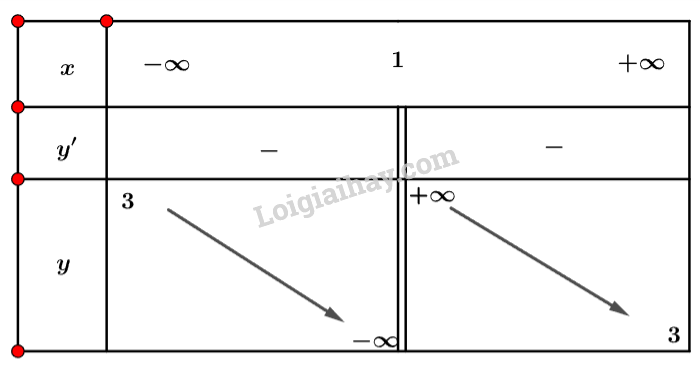
Vậy hàm số không có điểm cực trị.
Bài tập
Bài 1 trang 13 Toán 12 Tập 1: Cho hàm số có bảng biến thiên như sau:
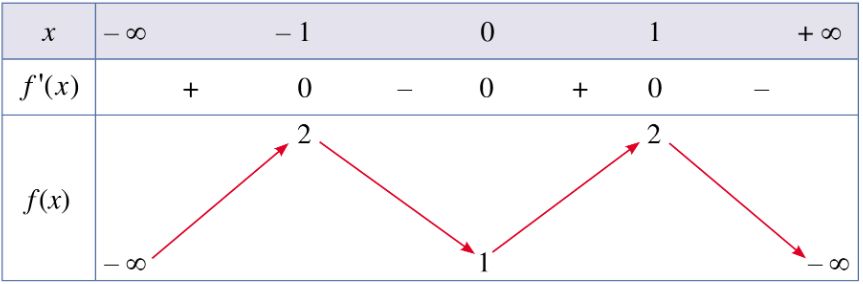
Hàm số đồng biến trên khoảng nào dưới đây?
A. .
B. .
C. .
D. .
Lời giải:
Dựa vào bảng biến thiên ta thấy đồ thị hàm số đi lên trong khoảng nên hàm số đồng biến trên khoảng .
Bài 2 trang 13 Toán 12 Tập 1: Cho hàm số có bảng biến thiên như sau:
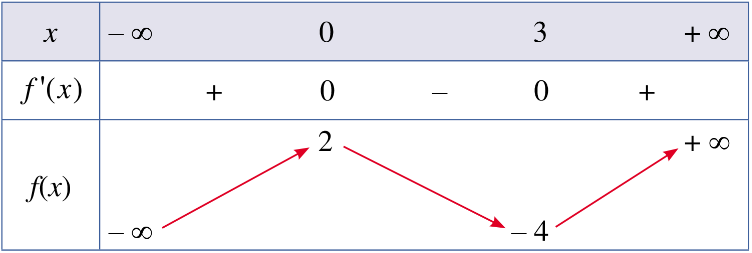
Giá trị cực tiểu của hàm số đã cho bằng:
a) .
b) .
c) .
d) .
Lời giải:
Giá trị cực tiểu của hàm số là
Bài 3 trang 13 Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số sau:
a) b)
c) d)
Lời giải:
a) Tập xác định: .
Ta có: .
Nhận xét
Ta có bảng biến thiên sau:
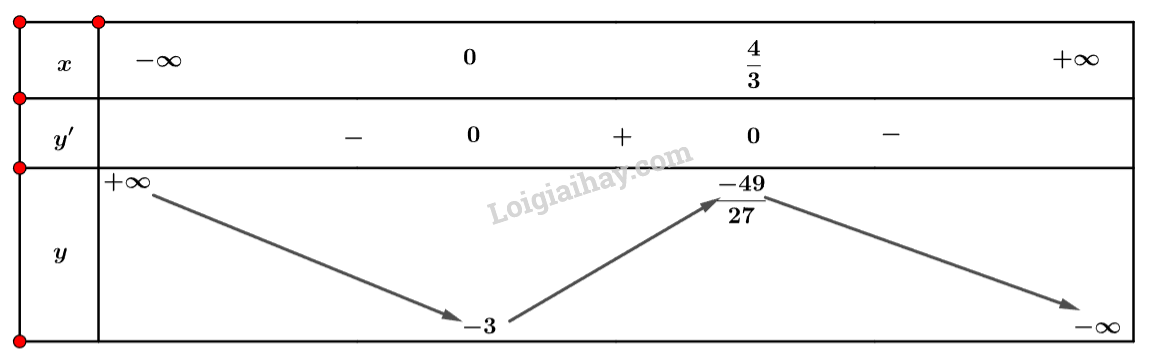
Vậy hàm số đồng biến trên khoảng và nghịch biến trên khoảng và .
b) Tập xác định: .
Ta có: .
Nhận xét
Ta có bảng biến thiên sau:
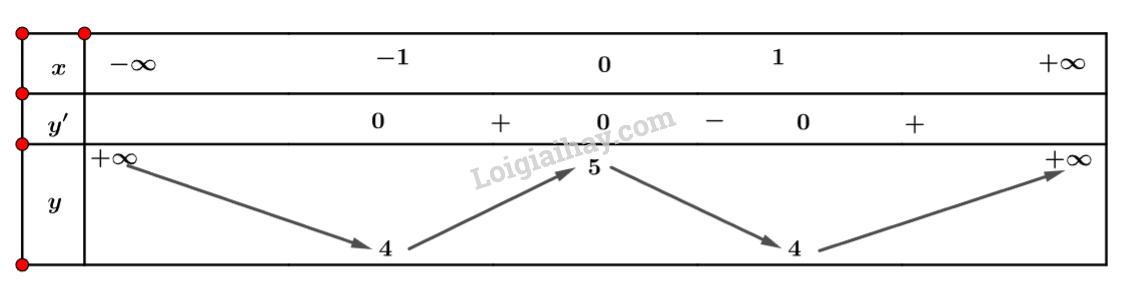
Vậy hàm số đồng biến trên khoảng và và nghịch biến trên khoảng và .
c) Tập xác định: .
Ta có: .
Nhận xét
Ta có bảng biến thiên sau:
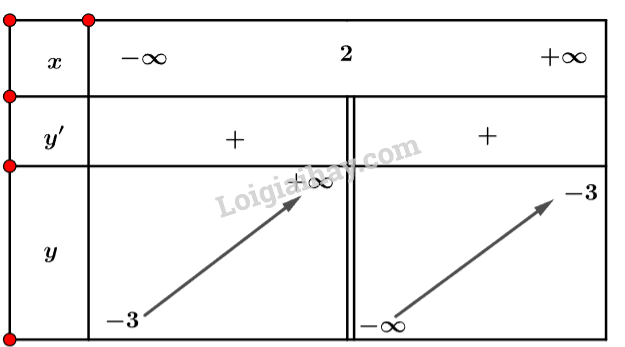
Vậy hàm số đồng biến trên khoảng và .
d) Tập xác định: .
Ta có: .
Nhận xét .
Ta có bảng biến thiên sau:
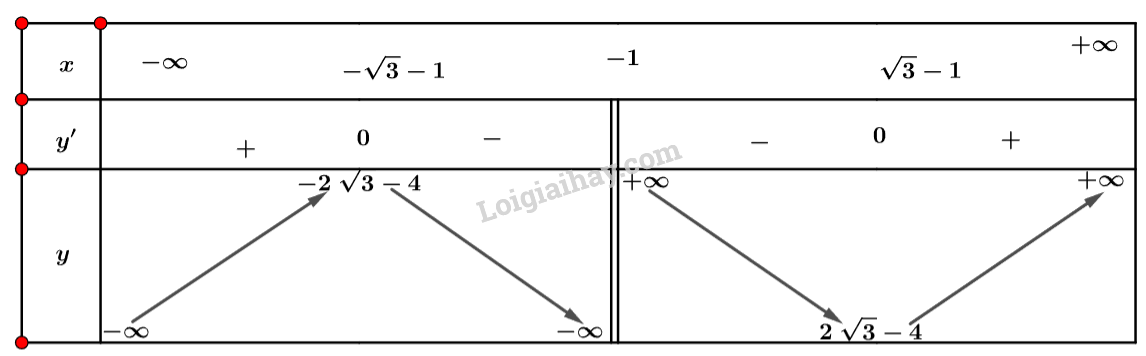
Vậy hàm số đồng biến trên khoảng và và nghịch biến trên khoảng và .
Bài 4 trang 13 Toán 12 Tập 1: Tìm cực trị của mỗi hàm số sau:
a)
b)
c)
Lời giải:
a) Tập xác định: .
Ta có: .
Nhận xét .
Ta có bảng biến thiên sau:
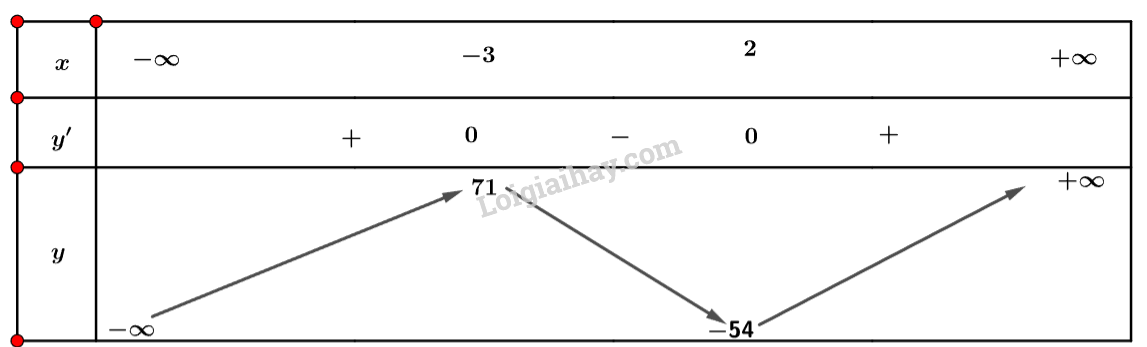
Vậy hàm số đạt cực đại tại điểm và đạt cực tiểu tại .
b) Tập xác định: .
Ta có: .
Nhận xét .
Ta có bảng biến thiên sau:
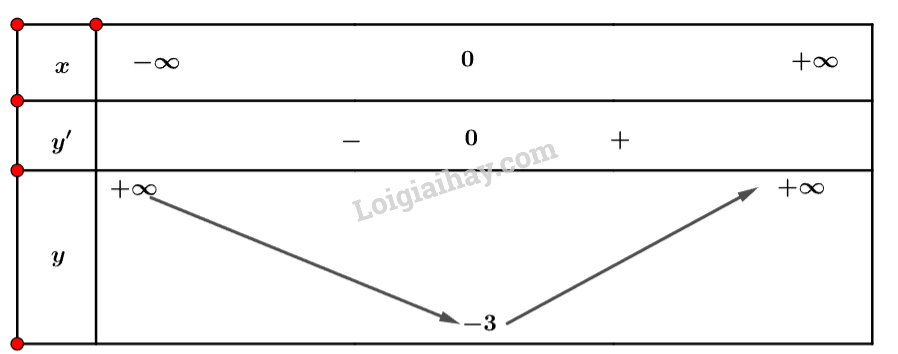
Vậy hàm số đạt cực tiểu tại
c) Tập xác định: .
Ta có: .
Nhận xét .
Ta có bảng biến thiên sau:
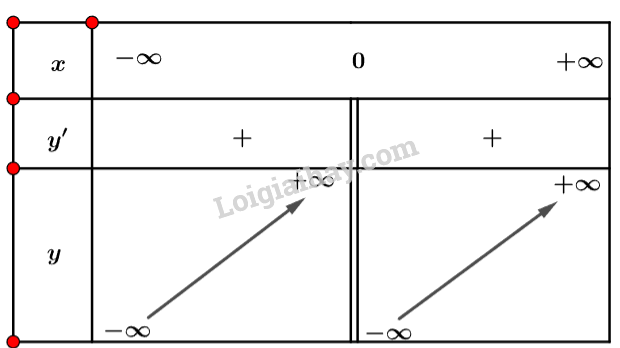
Vậy hàm số không có điểm tiểu và điểm cực đại.
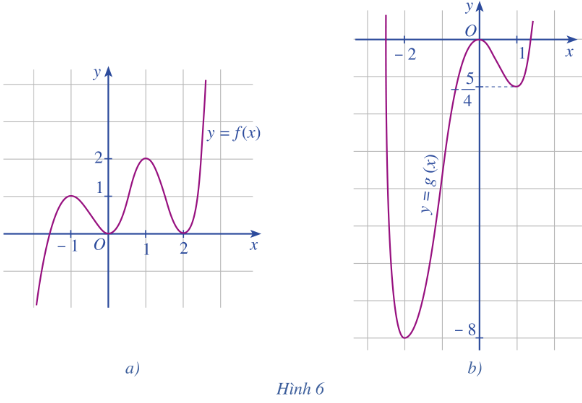
Bài 5 trang 14 Toán 12 Tập 1: Cho hai hàm số có đồ thị hàm số lần lượt ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
Lời giải:
a) Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
Hàm số đạt cực đại tại và . Hàm số đạt cực tiểu tại và .
b) Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
Hàm số đạt cực đại tại . Hàm số đạt cực tiểu tại và .
Bài 6 trang 14 Toán 12 Tập 1: Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T được tính bởi công thức sau:

Hỏi thể tích , giảm trong khoảng nhiệt độ nào?
Lời giải:

Ta có bảng biến thiên sau:
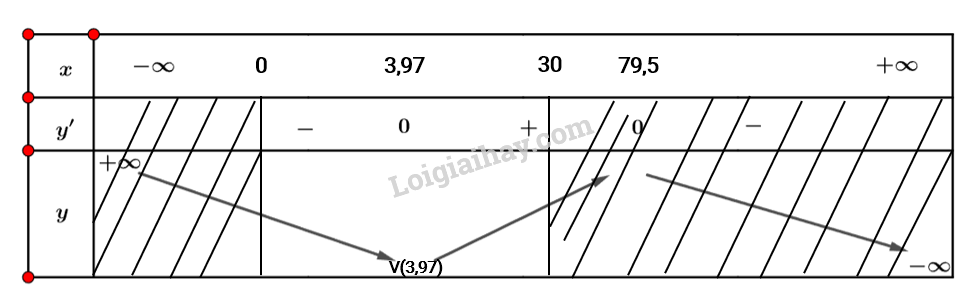
Vậy thể tích giảm trong khoảng nhiệt độ từ (0o; 3,97o).
Bài 7 trang 14 Toán 12 Tập 1: Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm cho đến khi tên lửa đẩy được phóng đi tại thời điểm , cho bởi hàm số sau:
.
(v được tính bằng ft/s, 1 feet = 0,3048 m)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Lời giải:
Tập xác định: .
Ta có: .
Nhận xét .
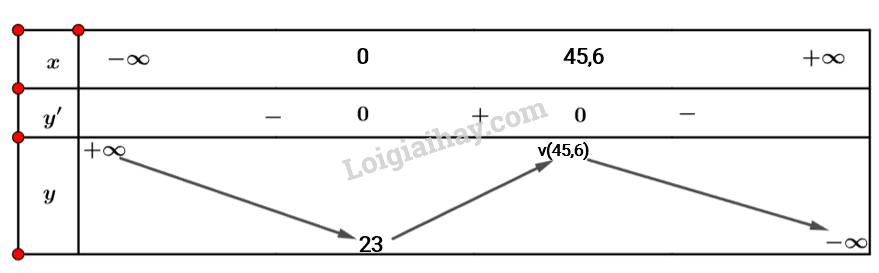
Vậy gia tốc tàu con thoi tăng trong khoảng 45,6s đầu tiên.
Xem thêm các bài giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:
§1. Tính đơn điệu của hàm số
§2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
§3. Đường tiệm cận của đồ thị hàm số
§4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Bài tập cuối chương 1
Chủ đề 1. Một số vấn đề về thuế
Lý thuyết Tính đơn điệu của hàm số
1. Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
Định lý 1
|
Cho hàm số y = f(x) có đạo hàm trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng – Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K – Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K |
Ví dụ: Hàm số y = |x| đồng biến trên khoảng , nghịch biến trên khoảng
Định lý 2
|
Cho hàm số y = f(x) có đạo hàm trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu f’(x) 0 (hoặc f’(x) 0) với mọi x thuộc K và f’(x) = 0 chỉ tại một số hữa hạn điểm của K thì hàm số f(x) đồng biến (hoặc nghịch biến) trên K |
Ví dụ: Hàm số có y’ = 2x – 4
y’ > 0 với nên HS đồng biến trên khoảng
y’ < 0 với nên HS đồng biến trên khoảng
2. Điểm cực trị, giá trị cực trị của hàm số
Khái niệm cực trị của hàm số
|
Cho hàm số y = f(x) liên tục trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng và – được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm sao cho (a;b) K và với mọi và . Khi đó, được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là – được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm sao cho (c;d) K và với mọi và . Khi đó, được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) |
Ví dụ: Cho đồ thị của hàm số y = f(x) như sau
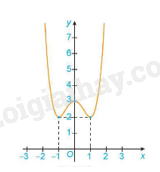
Hàm số đạt cực tiểu tại x = -1 và = y(-1) = 2
Hàm số đạt cực đại tại x = 0 và = y(0) = 3
Hàm số đạt cực tiểu tại x = 1 và = y(1) = 2
Định lý
|
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm và có đạo hàm trên các khoảng và . Khi đó: a) Nếu f’(x) < 0 với mọi và f’(x) > 0 với mọi thì hàm số f(x) đạt cực tiểu tại điểm b) Nếu f’(x) > 0 với mọi và f’(x) < 0 với mọi thì hàm số f(x) đạt cực tiểu tại điểm |
Ví dụ: Tìm cực trị của hàm số .
Tập xác định của hàm số là R.
Ta có: ; y’ = 0 x = 1 hoặc x = 3.
BBT:
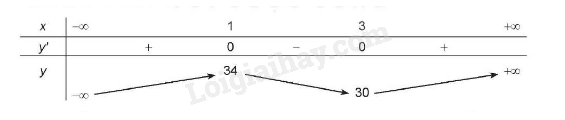
Hàm số đạt cực đại tại x = 1 và = y(1) = 34
Hàm số đạt cực tiểu tại x = 3 và = y(3) = 30


