Giải SGK Toán 12 Bài 3 (Cánh diều): Đường tiệm cận của đồ thị hàm số

Giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số

Hoạt động 1 trang 21 Toán 12 Tập 1: Xét hàm số $y=f\left(x\right)=\frac{26x+10}{x+5}$ với $x\in [0;+\mathrm{\infty })$ có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm $\underset{x\to +\mathrm{\infty }}{lim}f\left(x\right)$.

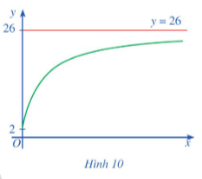
Lời giải:

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}f\left(x\right)=26$

Luyện tập 1 trang 22 Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số $y=\frac{3x-2}{x+1}$.

Lời giải:

Tập xác định $D=\mathbb{R}\mathrm{\setminus }\left\{-1\right\}$.

Ta có: $\{\begin{array}{l}\underset{x\to +\mathrm{\infty }}{lim}y=\underset{x\to +\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=3\\ \underset{x\to -\mathrm{\infty }}{lim}y=\underset{x\to -\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=3\end{array}$.

Vậy đường thẳng $y=3$ là tiệm cận ngang của đồ thị hàm số đã cho

Hoạt động 2 trang 22 Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=\frac{1}{x}$ có đồ thị là đường cong như Hình 12. Tìm $\underset{x\to 0^{+}}{lim}f\left(x\right),\underset{x\to 0^{-}}{lim}f\left(x\right)$

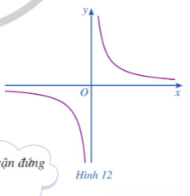
Lời giải:

Ta có: $\underset{x\to 0^{+}}{lim}f\left(x\right)=+\mathrm{\infty };\underset{x\to 0^{-}}{lim}f\left(x\right)=-\mathrm{\infty }$.

Luyện tập 2 trang 23 Toán 12 Tập 1: Tìm tiệm cận đứng của đồ thị hàm số $y=\frac{x^2+3x}{x-5}$.

Lời giải:

Tập xác định $D=\mathbb{R}\mathrm{\setminus }\left\{5\right\}$.

Ta có: $\{\begin{array}{l}\underset{x\to 5^{-}}{lim}y=\underset{x\to 5^{-}}{lim}\frac{x^2+3x}{x-5}=-\mathrm{\infty }\\ \underset{x\to 5^{+}}{lim}y=\underset{x\to 5^{+}}{lim}\frac{x^2+3x}{x-5}=+\mathrm{\infty }\end{array}$

Vậy đường thẳng $x=5$ là tiệm cận đứng của đồ thị hàm số đã cho

Hoạt động 3 trang 24 Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=x+1+\frac{1}{x-1}$ có đồ thị $\left(C\right)$ và đường thẳng $y=x+1$ (Hình 15). Tìm $\underset{x\to +\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(x+1\right)\right];\underset{x\to -\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(x+1\right)\right]$

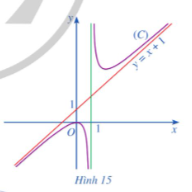
Lời giải:

Ta có: $\{\begin{array}{l}\underset{x\to +\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(x+1\right)\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x-1}=0\\ \underset{x\to -\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(x+1\right)\right]=\underset{x\to -\mathrm{\infty }}{lim}\frac{1}{x-1}=0\end{array}$

Luyện tập 3 trang 25 Toán 12 Tập 1: Chứng minh rằng đường thẳng $y=-x$ là tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{-x^2-2x+3}{x+2}$.

Lời giải:

Ta có: $y=f\left(x\right)=\frac{-x^2-2x+3}{x+2}=-x+\frac{3}{x+2}$.

Xét $\underset{x\to +\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(-x\right)\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{3}{x+2}=0$.

Vậy đường thẳng $y=-x$ là đường tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{-x^2-2x+3}{x+2}$

Luyện tập 4 trang 26 Toán 12 Tập 1: Tìm tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{x^2-3x+2}{x+3}$.

Lời giải:

Ta có: $y=f\left(x\right)=\frac{x^2-3x+2}{x+3}=x-6+\frac{20}{x+3}$.

Xét $\underset{x\to +\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(x-6\right)\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{20}{x+3}=0$.

Vậy đường thẳng $y=x-6$ là đường tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{x^2-3x+2}{x+3}$

Bài tập

Bài 1 trang 27 Toán 12 Tập 1: Tiệm cận đứng của đồ thị hàm số $y=\frac{x+2}{x+1}$ là:

A. $x=-1$.

B. $x=-2$.

C. $x=1$.

D. $x=2$.

Lời giải:

Ta có: $D=R\mathrm{\setminus }\left\{-1\right\}$

Xét $\underset{x\to -1^{+}}{lim}y=\underset{x\to -1^{+}}{lim}\frac{x+2}{x+1}=+\mathrm{\infty }$.

Vậy đưởng thẳng $x=-1$ là tiệm cận đứng của đồ thị hàm số $y=\frac{x+2}{x+1}$.

Chọn A

Bài 2 trang 27 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số $y=\frac{x^2+3x+5}{x+2}$ là:

A. $y=x$.

B. $y=x+1$.

C. $y=x+2$.

D. $y=x+3$.

Lời giải:

Ta có: $y=\frac{x^2+3x+5}{x+2}=x+1+\frac{3}{x+2}$

Xét $\underset{x\to +\mathrm{\infty }}{lim}\left[y-\left(x-6\right)\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{3}{x+2}=0$

Vậy đường thẳng $y=x+1$ là đường tiệm cận xiên của đồ thị hàm số $y=\frac{x^2+3x+5}{x+2}$

Bài 3 trang 27 Toán 12 Tập 1: Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau đây?

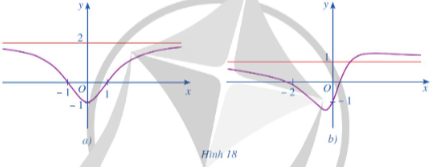
a) $y=\frac{x^2+2x-1}{x^2+1}$.

b) $y=\frac{2x^2+x+1}{x-1}$

c) $y=\frac{2x^2-2}{x^2+2}$

Lời giải:

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}y=\underset{x\to -\mathrm{\infty }}{lim}y=\frac{2x^2-2}{x^2+2}=2$. Do đó đường thẳng $y=2$ là một đường tiệm cận ngang của đồ thị hàm số $y=\frac{2x^2-2}{x^2+2}$. Vậy đồ thị hàm số $y=\frac{2x^2-2}{x^2+2}$ là hình 18a.

Tương tự, $\underset{x\to +\mathrm{\infty }}{lim}y=\underset{x\to -\mathrm{\infty }}{lim}y=\frac{x^2+2x-1}{x^2+1}=1$. Do đó đường thẳng $y=1$ là một đường tiệm cận ngang của đồ thị hàm số $y=\frac{x^2+2x-1}{x^2+1}$. Vậy đồ thị hàm số $y=\frac{x^2+2x-1}{x^2+1}$ là hình 18b.

Bài 4 trang 27 Toán 12 Tập 1: Tìm tiệm cận đứng, ngang, xiên (nếu có) của đồ thị mỗi hàm số sau:

a) $y=\frac{x}{2-x}$

b) $y=\frac{2x^2-3x+2}{x-1}$

c) $y=x-3+\frac{1}{x^2}$

Lời giải:

a) Tập xác định: $D=\mathbb{R}\mathrm{\setminus }\left\{2\right\}$.

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}y=\underset{x\to -\mathrm{\infty }}{lim}y=\frac{x}{2-x}=-1$

Mặt khác, $\{\begin{array}{l}\underset{x\to 2^{-}}{lim}y=\underset{x\to 2^{-}}{lim}\frac{x}{2-x}=+\mathrm{\infty }\\ \underset{x\to 2^{+}}{lim}y=\underset{x\to 2^{+}}{lim}\frac{x}{2-x}=-\mathrm{\infty }\end{array}$

Vậy đường thẳng $y=-1$ và $x=2$ lần lượt là đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\frac{x}{2-x}$.

b) Tập xác định: $D=\mathbb{R}\mathrm{\setminus }\left\{1\right\}$.

Ta có: $\{\begin{array}{l}\underset{x\to 1^{-}}{lim}y=\underset{x\to 1^{-}}{lim}\frac{2x^2-3x+2}{x-1}=-\mathrm{\infty }\\ \underset{x\to 1^{+}}{lim}y=\underset{x\to 1^{+}}{lim}\frac{2x^2-3x+2}{x-1}=+\mathrm{\infty }\end{array}$

Mặt khác, $y=\frac{2x^2-3x+2}{x-1}=2x-1+\frac{1}{x-1}$

Xét $\underset{x\to +\mathrm{\infty }}{lim}\left[y-\left(2x-1\right)\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x-1}=0$

Vậy đường thẳng $x=1$ và đường thẳng $y=2x-1$ lần lượt là tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y=\frac{2x^2-3x+2}{x-1}$

c) Tập xác định: $D=\mathbb{R}\mathrm{\setminus }\left\{0\right\}$.

Ta có: $\{\begin{array}{l}\underset{x\to 0^{-}}{lim}y=\underset{x\to 0^{-}}{lim}\left(x-3+\frac{1}{x^2}\right)=+\mathrm{\infty }\\ \underset{x\to 0^{+}}{lim}y=\underset{x\to 0^{+}}{lim}\left(x-3+\frac{1}{x^2}\right)=+\mathrm{\infty }\end{array}$.

Xét$$\underset{x\to +\mathrm{\infty }}{lim}\left[y-\left(x-3\right)\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x^2}=0$$

Vậy đường thẳng $x=0$ và đường thẳng $y=x-3$ lần lượt là tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y=x-3+\frac{1}{x^2}$

Bài 5 trang 27 Toán 12 Tập 1: Số lượng sản phẩm bán được cho một công ty trong x (tháng) được tính theo công thức

$S\left(x\right)=200\left(5-\frac{9}{2+x}\right)$ trong đó $x\ge 1$.

a) Xem $y=S\left(x\right)$ là một hàm số xác định trên nửa khoảng $[1;+\mathrm{\infty })$, hãy tìm tiệm cận ngang của đồ thị hàm số đó.

b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.

Lời giải:

a) Ta có: $\underset{x\to +\mathrm{\infty }}{lim}S\left(x\right)=\underset{x\to -\mathrm{\infty }}{lim}S\left(x\right)=1000$

Vậy đường thẳng $y=1000$ là đường tiệm cận ngang của đồ thị hàm số $S\left(x\right)$

b) Khi x đủ lớn thì số lượng sản phẩm bán được của công ti đó trong tháng x sẽ gần đạt được 1000 sản phẩm

Xem thêm các bài giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

§2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

§3. Đường tiệm cận của đồ thị hàm số

§4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài tập cuối chương 1

Chủ đề 1. Một số vấn đề về thuế

§1. Vectơ và các phép toán vectơ trong không gian

Lý thuyết Đường tiệm cận của đồ thị hàm số

1. Đường tiệm cận ngang

Đường thẳng $y=y_0$ gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=y_0$ hoặc $\underset{x\to -\mathrm{\infty }}{lim}f(x)=y_0$

Ví dụ: Tìm TCN của đồ thị hàm số $y=f(x)=\frac{3x-2}{x+1}$

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=\underset{x\to -\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=3$

Vậy đồ thị hàm số f(x) có TCN là y = 3.

2. Đường tiệm cận đứng

Đường thẳng $x=x_0$ gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:$\underset{x\to {x_0}^{+}}{lim}f(x)=+\mathrm{\infty };\underset{x\to {x_0}^{+}}{lim}f(x)=-\mathrm{\infty };\underset{x\to {x_0}^{-}}{lim}f(x)=+\mathrm{\infty };\underset{x\to {x_0}^{-}}{lim}f(x)=-\mathrm{\infty }$;

Ví dụ: Tìm TCĐ của đồ thị hàm số $y=f(x)=\frac{3-x}{x+2}$

Ta có: $\underset{x\to -2^{+}}{lim}\frac{3x-2}{x+2}=+\mathrm{\infty }$

Vậy đồ thị hàm số có TCĐ là x = -2

3. Đường tiệm cận xiên

Đường thẳng $y=ax+b(a\ne 0)$ gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=\left[f(x)-(ax+b)\right]=0$ hoặc $\underset{x\to -\mathrm{\infty }}{lim}f(x)=\left[f(x)-(ax+b)\right]=0$

Ví dụ: Tìm TCX của đồ thị hàm số $y=f(x)=x+\frac{1}{x+2}$

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}\left[f(x)-x\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x+2}=0$

Vậy đồ thị hàm số có TCX là y = x