Giải SGK Toán 12 Bài 1 (Cánh diều): Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

Giải bài tập Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

Câu hỏi khởi động trang 84 Toán 12 Tập 1: Bảng 1 là bảng tần số ghép nhóm biểu diễn mẫu số liệu ghi lại năng suất lúa (đơn vị: tạ/ha) của 60 địa phương.

Khoảng biến thiên của mẫu số liệu ghép nhóm được xác định như thế nào?

Lời giải:

Sau bài học này, ta sẽ giải quyết được bài toán trên như sau:

Trong mẫu số liệu ghép nhóm ở Bảng 1, ta có: đầu mút trái của nhóm 1 là a₁ = 40, đầu mút phải của nhóm 5 là a₆ = 75.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

R = a₆ – a₁ = 75 – 40 = 35.

Hoạt động 1 trang 84 Toán 12 Tập 1: Xét mẫu số liệu ghép nhóm cho bởi Bảng 2.

a) Tìm a₁, a₆ lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm 5.

b) Tính hiệu R = a₆ – a₁.

Lời giải:

a) Đầu mút trái của nhóm 1 là a₁ = 40.

Đầu mút phải của nhóm 5 là a₆ = 65.

b) Ta có R = a₆ – a₁ = 65 – 40 = 25.

Hoạt động 2 trang 86 Toán 12 Tập 1: Xét mẫu số liệu ghép nhóm cho bởi Bảng 5.

– Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4} = \frac{36}{4} = 9$ có đúng không?

– Tìm đầu mút trái s, độ dài h, tần số n₂ của nhóm 2; tần số tích lũy cf₁ của nhóm 1. Sau đó, hãy tính tứ phân vị thứ nhất Q₁ của mẫu số liệu đã cho theo công thức sau:

$Q_{1} = s + (\frac{9 - c f_{1}}{n_{2}}) \cdot h$ .

– Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{2} = \frac{36}{2} = 18$ có đúng không?

– Tìm đầu mút trái r, độ dài d, tần số n₃ của nhóm 3; tần số tích lũy cf₂ của nhóm 2. Sau đó, hãy tính tứ phân vị thứ hai Q₂ của mẫu số liệu đã cho theo công thức sau:

$Q_{2} = r + (\frac{18 - c f_{2}}{n_{3}}) \cdot d$ .

– Nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{3 n}{4} = \frac{3 \cdot 36}{4} = 27$ có đúng không?

– Tìm đầu mút trái t, độ dài l, tần số n₄ của nhóm 4; tần số tích lũy cf₃ của nhóm 3. Sau đó, hãy tính tứ phân vị thứ hai Q₃ của mẫu số liệu đã cho theo công thức sau:

$Q_{2} = t + (\frac{27 - c f_{3}}{n_{4}}) \cdot l$ .

d) Tìm hiệu Q₃ – Q₁.

Lời giải:

a) – Tần số tích lũy của nhóm 1 là 6 < 9, tần số tích lũy của nhóm 2 là 17 > 9.

Vậy nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4} = \frac{36}{4} = 9$ .

– Nhóm 2 có đầu mút trái s = 163, độ dài h = 163 – 160 = 3, tần số n₂ = 11; tần số tích lũy của nhóm 1 là cf₁ = 6.

Tứ phân vị thứ nhất Q₁ của mẫu số liệu đã cho là

$Q_{1} = s + (\frac{9 - c f_{1}}{n_{2}}) \cdot h = 163 + (\frac{9 - 6}{11}) \cdot 3 = \frac{1802}{11} \approx 163, 82$ .

b) – Tần số tích lũy của nhóm 1 là 6 < 18, tần số tích lũy của nhóm 2 là 17 < 18, tần số tích lũy của nhóm 3 là 26 > 18.

Vậy nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{2} = \frac{36}{2} = 18$ .

– Nhóm 3 có đầu mút trái r = 166, độ dài d = 169 – 166 = 3, tần số n₃ = 9; tần số tích lũy của nhóm 2 là cf₂ = 17.

Tứ phân vị thứ hai Q₂ của mẫu số liệu đã cho là

$Q_{2} = r + (\frac{18 - c f_{2}}{n_{3}}) \cdot d = 166 + (\frac{18 - 17}{9}) \cdot 3 = \frac{499}{3} \approx 166, 33$ .

c) – Tần số tích lũy của nhóm 1 là 6 < 27, tần số tích lũy của nhóm 2 là 17 < 27, tần số tích lũy của nhóm 3 là 26 < 27, tần số tích lũy của nhóm 4 là 33 > 27.

Vậy nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{3 n}{4} = \frac{3 \cdot 36}{4} = 27$ .

– Nhóm 4 có đầu mút trái t = 169, độ dài l = 172 – 169 = 3, tần số n₄ = 7; tần số tích lũy của nhóm 3 là cf₃ = 26.

Tứ phân vị thứ ba Q₃ của mẫu số liệu đã cho là

$Q_{3} = t + (\frac{27 - c f_{3}}{n_{4}}) \cdot l = 169 + (\frac{27 - 26}{7}) \cdot 3 = \frac{1186}{7} \approx 169, 43$ .

d) Ta có Q₃ – Q₁ = $\frac{1186}{7} - \frac{1802}{11} = \frac{432}{77}$ ≈ 5,61.

Luyện tập 2 trang 87 Toán 12 Tập 1: Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi Bảng 1 trong phần mở đầu.

Lời giải:

Từ Bảng 1 ta có bảng sau:

Số phần tử của mẫu là n = 60.

– Ta có: $\frac{n}{4} = \frac{60}{4} = 15$ mà 7 < 15 < 28. Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 3 là nhóm [54; 61) có s = 54; h = 7; n₃ = 21 và nhóm 2 là nhóm [47; 54) có cf₂ = 7.

Áp dụng công thức, ta có tứ phân vị thứ nhất là

$Q_{1} = 54 + (\frac{15 - 7}{21}) \cdot 7 = \frac{170}{3}$ (tạ/ha).

– Ta có: $\frac{3 n}{4} = \frac{3 \cdot 60}{4} = 45$ mà 28 < 45 < 49. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [61; 68) có t = 61; l = 7; n₄ = 21 và nhóm 3 là nhóm [54; 61) có cf₃ = 28.

Áp dụng công thức, ta có tứ phân vị thứ ba là

$Q_{3} = 61 + (\frac{45 - 28}{21}) \cdot 7 = \frac{200}{3}$ (tạ/ha).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = $\frac{200}{3} - \frac{170}{3}$ = 10 (tạ/ha).

Bài tập

Bài 1 trang 88 Toán 12 Tập 1: Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

A. 50.

B. 30.

C. 6.

D. 69,8.

b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:

A. 50.

B. 40.

C. 14,23.

D. 70,87.

Lời giải:

a) Đáp án đúng là: A

Trong mẫu số liệu ghép nhóm ở Bảng 8, ta có: đầu mút trái của nhóm 1 là a₁ = 40, đầu mút phải của nhóm 5 là a₆ = 90.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

R = a₆ – a₁ = 90 – 40 = 50 (nghìn đồng).

b) Đáp án đúng là: C

Từ Bảng 8 ta có bảng sau:

Số phần tử của mẫu là n = 60.

– Ta có: $\frac{n}{4} = \frac{60}{4} = 15$ mà 9 < 15 < 28. Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 3 là nhóm [60; 70) có s = 60; h = 10; n₃ = 19 và nhóm 2 là nhóm [50; 60) có cf₂ = 9.

Áp dụng công thức, ta có tứ phân vị thứ nhất là

$Q_{1} = 60 + (\frac{15 - 9}{19}) \cdot 10 = \frac{1200}{19}$ (nghìn đồng).

– Ta có: $\frac{3 n}{4} = \frac{3 \cdot 60}{4} = 45$ mà 28 < 45 < 51. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [70; 80) có t = 70; l = 10; n₄ = 23 và nhóm 3 là nhóm [60; 70) có cf₃ = 28.

Áp dụng công thức, ta có tứ phân vị thứ ba là

$Q_{3} = 70 + (\frac{45 - 28}{23}) \cdot 10 = \frac{1780}{23}$ (nghìn đồng).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = $\frac{1780}{23} - \frac{1200}{19}$ ≈ 14,23 (nghìn đồng).

Bài 2 trang 88 Toán 12 Tập 1: Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng).

a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.

b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.

Lời giải:

a) Trong mẫu số liệu ghép nhóm ở Bảng 9, ta có: đầu mút trái của nhóm 1 là a₁ = 10, đầu mút phải của nhóm 6 là a₇ = 40.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

R = a₇ – a₁ = 40 – 10 = 30 (triệu đồng).

b) Từ Bảng 9 ta có bảng sau:

Số phần tử của mẫu là n = 60.

– Ta có: $\frac{n}{4} = \frac{60}{4} = 15$ . Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 1 là nhóm [10; 15) có s = 10; h = 5; n₁ = 15.

Áp dụng công thức, ta có tứ phân vị thứ nhất là

$Q_{1} = 10 + \frac{15}{15} \cdot 5 = 15$ (triệu đồng).

– Ta có: $\frac{3 n}{4} = \frac{3 \cdot 60}{4} = 45$ mà 43 < 45 < 53. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [25; 30) có t = 25; l = 5; n₄ = 10 và nhóm 3 là nhóm [20; 25) có cf₃ = 43.

Áp dụng công thức, ta có tứ phân vị thứ ba là

$Q_{3} = 25 + (\frac{45 - 43}{10}) \cdot 5 = 26$ (triệu đồng).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = 26 – 15 = 11 (triệu đồng).

Bài 3 trang 88 Toán 12 Tập 1: Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.

a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.

b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.

Lời giải:

a) Trong mẫu số liệu ghép nhóm ở Bảng 10, ta có: đầu mút trái của nhóm 1 là a₁ = 20, đầu mút phải của nhóm 6 là a₇ = 80.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

R = a₇ – a₁ = 80 – 20 = 60.

b) Từ Bảng 10 ta có bảng sau:

Số phần tử của mẫu là n = 100.

– Ta có: $\frac{n}{4} = \frac{100}{4} = 25$ . Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25. Xét nhóm 1 là nhóm [20; 30) có s = 20; h = 10; n₁ = 25.

Áp dụng công thức, ta có tứ phân vị thứ nhất là

$Q_{1} = 20 + \frac{25}{25} \cdot 10 = 30$ .

– Ta có: $\frac{3 n}{4} = \frac{3 \cdot 100}{4} = 75$ mà 65 < 75 < 80. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75. Xét nhóm 4 là nhóm [50; 60) có t = 50; l = 10; n₄ = 15 và nhóm 3 là nhóm [40; 50) có cf₃ = 65.

Áp dụng công thức, ta có tứ phân vị thứ ba là

$Q_{3} = 50 + (\frac{75 - 65}{15}) \cdot 10 = \frac{170}{3}$ .

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = $\frac{170}{3} - 30 = \frac{80}{3}$ ≈ 26,67.

Xem thêm các bài giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 2

§1. Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

§2. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

Bài tập cuối chương 3

§1. Nguyên hàm

§2. Nguyên hàm của mốt số hàm số sơ cấp

Lý thuyết Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

1. Khoảng biến thiên

a) Định nghĩa

Xét mẫu số liệu ghép nhóm cho trong bảng sau, trong đó $n_{1} > 0$ và $n_{m} > 0$ .

Gọi $a_{1}, a_{m + 1}$ lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm m.

Hiệu $R = a_{m + 1} - a_{1}$ được gọi là khoảng biến thiên của mẫu số liệu ghép nhóm đó

b) Ý nghĩa

Khoảng biến thiên của mẫu số liệu ghép nhóm đo mức độ phân tán của mẫu số đó. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán
Trong các đại lượng đo mức độ phân tán của mẫu số liệu ghép nhóm, khoảng biến thiên là đại lượng dễ hiểu, dễ tính toán. Tuy nhiên, do khoảng biến thiên chỉ sử dụng hai giá trị của mẫu số liệu nên đại lượng đó dễ bị ảnh hưởng bởi các giá trị bất thường
Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc.

2. Khoảng tứ phân vị

a) Định nghĩa

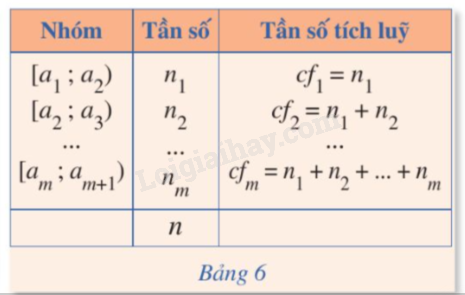
Xét mẫu số liệu ghép nhóm cho bởi bảng sau

Gọi $Q_{1}, Q_{2}, Q_{3}$ là tứ phân vị của mẫu số liệu đó. Ta gọi hiệu $Δ_{Q} = Q_{3} - Q_{1}$ là khoảng tứ phân vị của mẫu số liệu đó.

b) Ý nghĩa

Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị bất thường của mẫu đó. Khoảng tứ phân vị thường được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết các giá trị bất thường của mẫu số liệu và nó không bị ảnh hưởng bởi các giá trị bất thường đó.

Related Posts

Để lại một bình luận Huỷ trả lời