Sách bài tập Toán 12 Bài 1 (Chân trời sáng tạo): Vectơ và các phép toán trong không gian

Giải SBT Toán 12 Bài 1: Vectơ và các phép toán trong không gian

Bài 1 trang 62 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’.

a) Chỉ ra các vectơ có điểm đầu là B và điểm cuối là các đỉnh của hình hộp không cùng nằm trên một mặt của hình hộp với điểm B.

b) Tìm các vectơ bằng vectơ $\vec{B C}$ .

c) Tìm các vectơ đối của vectơ $\vec{B D}$

Lời giải:

a) Các vectơ có điểm đầu là B và điểm cuối là các đỉnh của hình hộp không cùng nằm trên một mặt của hình hộp với điểm B là: $\vec{B D^{‘}}$ .

b) Các vectơ bằng vectơ $\vec{B C}$ là $\vec{A D}, \vec{A^{‘} D^{‘}}, \vec{B^{‘} C^{‘}}$ .

c) Các vectơ đối của vectơ $\vec{B D}$ là $\vec{D B}, \vec{D^{‘} B^{‘}}$

Bài 2 trang 63 SBT Toán 12 Tập 1: Cho tứ diện OABC. Tính các vectơ:

a) $\vec{O A} + \vec{A B} - \vec{O C}$ ;

b) $\vec{O A} + \vec{O B} + \vec{O C}$ .

Lời giải:

a) Ta có: $\vec{O A} + \vec{A B} - \vec{O C}$ = $\vec{O B} - \vec{O C} = \vec{C B}$ .

b) Dựng hình hộp OADB.CFEK

Ta có: $\vec{O A} + \vec{O B} + \vec{O C}$ = $\vec{O D} + \vec{O C} = \vec{O E}$

Bài 3 trang 63 SBT Toán 12 Tập 1: Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc 120° và có độ lớn lần lượt là 10 N và 8 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn 6 N. Tính độ lớn của hợp lực của ba lực trên.

Lời giải:

Gọi $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ lần lượt là ba lực tác động vào một vật đặt tại điểm O như Hình 2.

Ta có: $\vec{F_{1}} = \vec{O A}$ , $\vec{F_{2}} = \vec{O B}$ , $\vec{F_{3}} = \vec{O C}$ .

Độ lớn các lực: F₁ = OA = 10 N, F₂ = OB = 8 N, F₃ = OC = 6 N.

Dựng hình bình hành OADB. Theo quy tắc hình bình hành, ta có: $\vec{O D} = \vec{O A} + \vec{O B}$ .

Suy ra ${\vec{O D}}^{2} = {(\vec{O A} + \vec{O B})}^{2} = {\vec{O A}}^{2} + {\vec{O B}}^{2} + 2 \vec{O A} . \vec{O B}$

Mà $\vec{O A} . \vec{O B}$ = OA.OB.cos $(\vec{O A}, \vec{O B})$

⇒ OD² = OA² + OB² + 2OA.OB.cos120°.

Dựng hình bình hành ODEC.

Tổng lực tác động vào vật là $\vec{F} = \vec{O E} = \vec{O A} + \vec{O B} + \vec{O C}$ .

Độ lớn của hợp lực tác động vào vật là F = OE.

Vì $O C ⊥ (O A D B)$ nên OC ⊥ OD, suy ra ODEC là hình chữ nhật.

Do đó, tam giác ODE vuông tại D.

Khi đó, OE² = OC² + OD² = OC² + OA² + OB² + 2OA.OB.cos120°.

Suy ra OE = $\sqrt{O C^{2} + O A^{2} + O B^{2} + 2. O A . O B \cos 120 °}$

= $\sqrt{6^{2} + 10^{2} + 8^{2} + 2.10.8. \cos 120 °}$ ≈ 10,95.

Do đó, F = OE ≈ 10,95 N.

Bài 4 trang 63 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ có AC’ và A’C cắt nhau tại O. Cho biết AO = a. Tính theo a độ dài các vectơ:

a) $\vec{A B} + \vec{A D} + \vec{A A^{‘}}$ ;

b) $\vec{C^{‘} B^{‘}} + \vec{C^{‘} D^{‘}} + \vec{A^{‘} A}$ .

Lời giải:

a) Theo quy tắc hình hộp, ta có: $\vec{A B} + \vec{A D} + \vec{A A^{‘}}$ = $\vec{A C^{‘}}$ .

Suy ra $|\vec{A B} + \vec{A D} + \vec{A A^{‘}}| = |\vec{A C^{‘}}|$ = AC’ = 2AO = 2a.

b) Ta có: $\vec{C^{‘} B^{‘}} + \vec{C^{‘} D^{‘}} + \vec{A^{‘} A}$ = $\vec{C^{‘} B^{‘}} + \vec{C^{‘} D^{‘}} + \vec{C^{‘} C} = \vec{C^{‘} A}$

Suy ra $|\vec{C^{‘} B^{‘}} + \vec{C^{‘} D^{‘}} + \vec{A^{‘} A}| = |\vec{C^{‘} A}| = C^{‘} A = 2 a$ .

Bài 5 trang 63 SBT Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’. Gọi O, O’ lần lượt là tâm của các hình vuông ABCD và A’B’C’D’; I là giao điểm của AC’ và A’C.

Chứng minh rằng:

a) $\vec{O A^{‘}} + \vec{O B^{‘}} + \vec{O C^{‘}} + \vec{O D^{‘}} = 4 \vec{O O^{‘}}$ ;

b) $\vec{D B} + \vec{D D^{‘}} = 2 \vec{D I}$ .

Lời giải:

a) Ta có: $\vec{O A^{‘}} + \vec{O B^{‘}} + \vec{O C^{‘}} + \vec{O D^{‘}}$ = $(\vec{O A^{‘}} + \vec{O C^{‘}}) + (\vec{O B^{‘}} + \vec{O D^{‘}})$ = $2 \vec{O O^{‘}} + 2 \vec{O O^{‘}}$ = $4 \vec{O O^{‘}}$ .

b) Ta có bốn đường chéo của hình lập phương cắt nhau tại trung điểm I của mỗi đường chéo nên I cũng là trung điểm của DB’. Suy ra $\vec{D B} + \vec{D D^{‘}} = \vec{D B^{‘}} = 2 \vec{D I}$ .

Bài 6 trang 63 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và cho biết $\hat{B A D} = \hat{B A A^{‘}} = \hat{D A A^{‘}}$ = 60°. Tính các tích vô hướng sau:

a) $\vec{A B} . \vec{A D}$ ;

b) $\vec{D A} . \vec{D C}$ ;

c) $\vec{A A^{‘}} . \vec{A C}$

Lời giải:

Bài 7 trang 64 SBT Toán 12 Tập 1: Một tàu kéo một xà lan trên biển di chuyển được 3 km với một lực kéo có cường độ 2 000 N và có phương hợp với phương dịch chuyển một góc 30°. Tính công thực hiện bởi lực kéo nói trên (kết quả làm tròn đến hàng đơn vị của Jun).

Lời giải:

Áp dụng công thức tính công, ta có:

A = $|\vec{F}| . |\vec{d}| . \cos (\vec{F}, \vec{d})$ = 2000.3000.cos30° ≈ 5 196 152 (J).

Bài 8 trang 64 SBT Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Gọi x, y, z theo thứ tự là số đo các góc hợp bởi vectơ $\vec{A C^{‘}}$ với các vectơ $\vec{A B}, \vec{A D}, \vec{A A^{‘}}$ .

Chứng minh cos²x + cos²y + cos²_Z = 1.

Lời giải:

Gọi a, b, c, d lần lượt là độ dài của AB, AD, AA’ và AC’.

Ta có: $A {C^{‘}}^{2} = A B^{2} + A D^{2} + A {A^{‘}}^{2}$

⇔ d² = a² + b² + c², cosx = $\frac{a}{d}$ , cosy = $\frac{b}{d}$ , cosz = $\frac{c}{d}$ .

Suy ra cos²x + cos²y + cos²z = ${(\frac{a}{d})}^{2} + {(\frac{b}{d})}^{2} + {(\frac{c}{d})}^{2}$ = $\frac{a^{2} + b^{2} + c^{2}}{d^{2}} = \frac{d^{2}}{d^{2}} = 1$ .

Vậy cos²x + cos²y + cos²_Z = 1.

Bài 9 trang 64 SBT Toán 12 Tập 1: Tính độ lớn của các lực căng trên mỗi sợi dây cáp trong Hình 16. Cho biết khối lượng xe là 1 900 kg, gia tốc là 10 m/s², khung nâng có khối lượng 100 kg và có dạng hình chóp S.ABCD với đáy ABCD là hình chữ nhật tâm O, AB = 8 m, BC = 12 m, SC = 12 m và SO vuông góc với (ABCD). Làm tròn kết quả đến hàng đơn vị của Newton.

Lời giải:

Ta có:

AC = BD = $\sqrt{A B^{2} + B C^{2}} = \sqrt{8^{2} + 12^{2}} = 4 \sqrt{13}$ ,

SO = $\sqrt{S C^{2} - O C 2}$ = $\sqrt{12^{2} - {(2 \sqrt{13})}^{2}}$ = $2 \sqrt{23}$ ,

sin $\hat{S C O}$ = $\frac{S O}{S C}$ = $\frac{2 \sqrt{23}}{12} = \frac{\sqrt{23}}{6}$ .

Gọi P là độ lớn của trọng lực xe và khung sắt nâng.

Ta có: P = (1900 + 100).10 = 20 000 (N).

Gọi F là độ lớn của lực căng trên mỗi sợi cáp.

Ta có: Fsin $\hat{S C O} = \frac{P}{4}$ , suy ra F = $\frac{P}{4 \sin \hat{S C O}} = \frac{20000}{4 \frac{\sqrt{23}}{6}}$ ≈ 6 255 (N).

Lý thuyết Vectơ và các phép toán trong không gian

1. Vecto trong không gian

Vecto trong không gian là một đoạn thẳng có hướng
Các khái niệm có liên quan đến vecto trong không gian như: giá của vecto, độ dài của vecto, vecto cùng phương, vecto cùng hướng, vecto-không, hai vecto bằng nhau, hai vecto đối nhau, … được phát biểu tương tự như trong mặt phẳng

2. Tổng và hiệu của hai vecto

a) Tổng của hai vecto

Trong không gian, cho hai vecto $\vec{a}$ và $\vec{b}$ . Lấy một điểm A bất kì và các điểm B,C sao cho $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Khi đó, vecto $\vec{A C}$ được gọi là tổng của hai vecto $\vec{a}$ và $\vec{b}$ , kí hiệu là $\vec{a} + \vec{b}$

Phép lấy tổng của hai vecto được gọi là phép cộng vecto

Với 3 điểm A, B, C trong không gian, ta có: $\vec{A B} + \vec{B C} = \vec{A C}$ (Quy tắc 3 điểm)
Nếu ABCD là hình bình hành thì $\vec{A B} + \vec{A D} = \vec{A C}$ (Quy tắc hình bình hành)
Nếu ABCD.A’B’C’D’ là hình hộp thì $\vec{A B} + \vec{A D} + \vec{A A^{'}} = \vec{A C^{'}}$ (Quy tắc hình hộp)

b) Hiệu của hai vecto

Trong không gian, cho hai vecto $\vec{a}$ và $\vec{b}$ . Hiệu của hai vecto $\vec{a}$ và $\vec{b}$ là tổng của hai vecto $\vec{a}$ và vecto đối của $\vec{b}$ , kí hiệu là $\vec{a} - \vec{b}$

Phép lấy hiệu của hai vecto được gọi là phép trừ vecto

Với ba điểm O, A, B trong không gian, ta có: $\vec{O A} - \vec{O B} = \vec{B A}$ (Quy tắc hiệu)

3. Tích của một số với một vecto

Trong không gian, tích của một số thực $k \neq 0$ với một vecto $\vec{a} \neq \vec{0}$ là một vecto, kí hiệu là $k \vec{a}$ , được xác định như sau:

– Cùng hướng với vecto $\vec{a}$ nếu k > 0; ngược hướng với vecto $\vec{a}$ nếu k < 0

– Có độ dài bằng $| k | . | \vec{a} |$

Phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto

4. Tích vô hướng của hai vecto

a) Góc giữa hai vecto trong không gian

Trong không gian, cho hai vecto

\vec{a}

và

\vec{b}

khác

\vec{0}

. Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho

\vec{O A} = \vec{a}, \vec{O B} = \vec{b}

. Khi đó, góc

\hat{A O B} (0^{\circ} \leq \hat{A O B} \leq 180^{\circ})

được gọi là góc giữa hai vecto

\vec{a}

và

\vec{b}

, kí hiệu

(\vec{a}, \vec{b})

b) Tích vô hướng của hai vecto

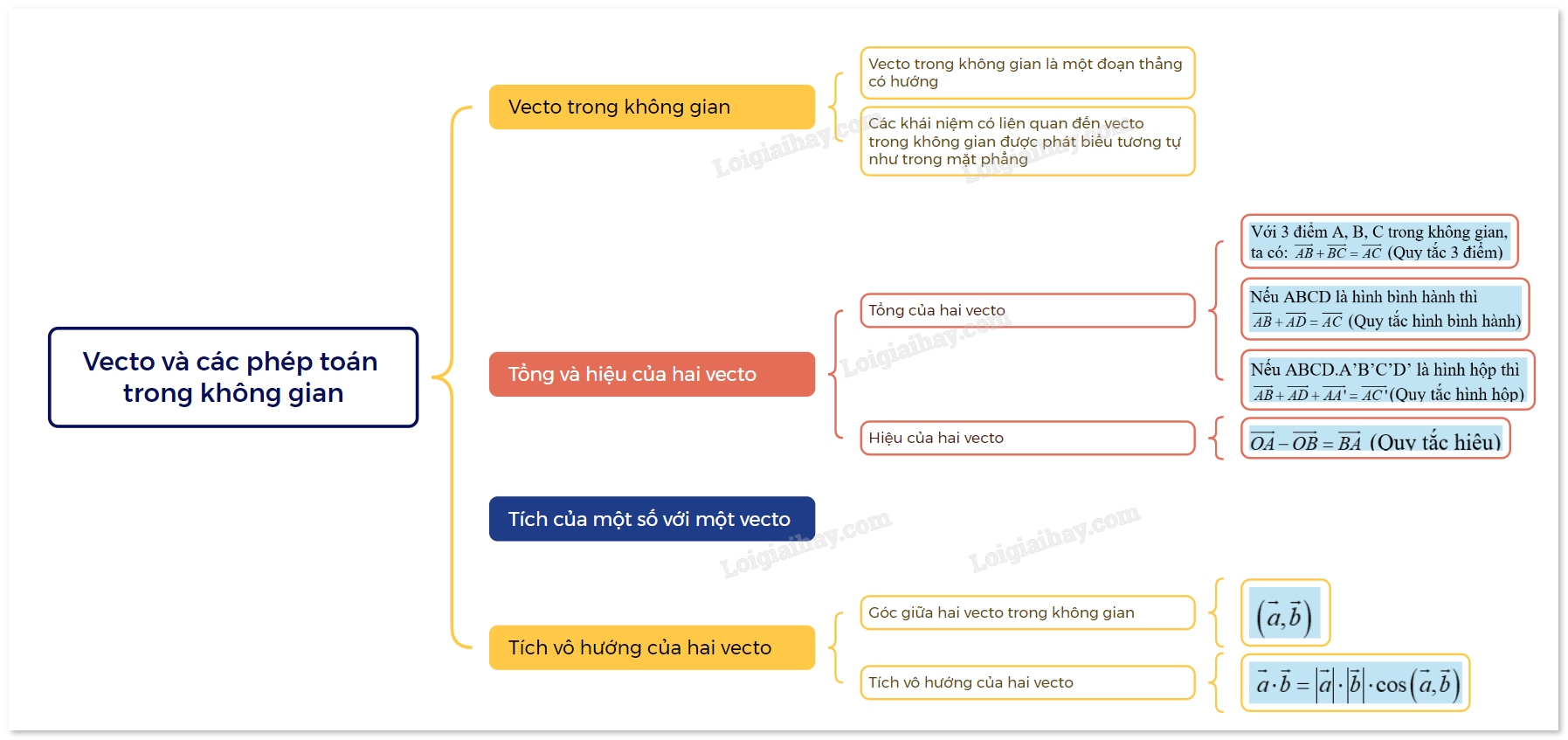
Trong không gian, cho hai vecto $\vec{a}$ và $\vec{b}$ khác $\vec{0}$ . Tích vô hướng của hai vecto $\vec{a}$ và $\vec{b}$ là một số, kí hiệu là $\vec{a} \cdot \vec{b}$ , được xác định bởi công thức $\vec{a} \cdot \vec{b} = | \vec{a} | \cdot | \vec{b} | \cdot \cos (\vec{a}, \vec{b})$

Sơ đồ tư duy Vectơ và các phép toán trong không gian

Xem thêm các bài giải SBT Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 1

Bài 1: Vectơ và các phép toán trong không gian

Bài 2: Toạ độ của vectơ trong không gian

Bài 3: Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2

Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm

Related Posts

Để lại một bình luận Huỷ trả lời