Giải SBT Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số
Bài 1.21 trang 19 SBT Toán 12 Tập 1: Cho hàm số . Đồ thị hàm số f(x) có tiệm cận đứng không?
Lời giải:
Ta có: = (x + 5) = 7.
Hơn nữa y = f(x) liên tục tại mọi điểm x ≠ 2. Do đó, đồ thị hàm f(x) không có tiệm cận đứng.
Bài 1.22 trang 19 SBT Toán 12 Tập 1: Tìm các đường tiệm cận của đồ thị các hàm số sau:
a) y =
b) y =
Lời giải:
a) Ta có: ;
.
Do đó, đường thẳng y = là tiệm cận ngang của đồ thị hàm số.
;
.
Do đó, đường thẳng x = là đường tiệm cận đứng của đồ thị hàm số.
b) Ta có: ;
.
Do đó, đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.
;
.
Do đó, đường thẳng x = −2 là đường tiệm cận đứng của đồ thị hàm số.
Bài 1.23 trang 19 SBT Toán 12 Tập 1: Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:
a)
b) y =
Lời giải:
a)
Ta có: ;
.
Do đó, đường thẳng x = 2 là đường tiệm cận đứng của đồ thị hàm số.
.
.
Do đó đường thẳng y = x + 1 là đường tiệm cận xiên của đồ thị hàm số.
b) y =
Ta có: ;
Do đó đường thẳng x = −3 là tiệm cận đứng của đồ thị hàm số.
.
.
Do đó đường thẳng y = 3x – 1 là tiệm cận xiên của đồ thị hàm số.
Bài 1.24 trang 19 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:
Hãy tìm các tiệm cận đứng và tiệm cận ngang và đồ thị hàm số đã cho.
Lời giải:
Dựa vào bảng biến thiên, ta thấy:
= −∞; = +∞.
Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
= 3, do đó đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.
Bài 1.25 trang 19 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:
Tìm các đường tiệm cận ngang của đồ thị hàm số
Lời giải:
Dựa vào bảng biến thiên, ta có: = 1 và = −1.
Suy ra = =
= = −1
Do đó, đường thẳng y = −1 và y = là hai đường tiệm cận ngang của đồ thị hàm số g(x).
Bài 1.26 trang 20 SBT Toán 12 Tập 1: Cho hàm số có đồ thị (C). Tính tích khoảng cách từ một điểm tùy ý thuộc (C) đến hai đường tiệm cận của nó.
Lời giải:
Ta có: ;
.
Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
;
.
Do đó đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng x = 1 và tiệm cận ngang y = 1.
Lấy M(x0; y0) ∈ (C) với .
Ta có: khoảng cách từ M đến đường tiệm cận đứng là d1 = | x0 – 1|, khoảng cách từ M đến tiệm cận ngang là d2 = .
Vậy tích khoảng cách là:d1d2 = . = 2.
Bài 1.27 trang 20 SBT Toán 12 Tập 1: Gọi I là giao điểm giữa tiệm cận đứng và tiệm cận ngang của đồ thị hàm số . Cho điểm K(3; 5), tính hệ số góc của đường thẳng qua I và K.
Lời giải:
Ta có: ;
.
Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
;
.
Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
Suy ra điểm I(2; 2).
Đường thẳng đi qua I(2; 2) và K(3; 5) có hệ số góc là: a = .
Vậy hệ số góc của đường thẳng đi qua hai điểm I và K là 3.
Bài 1.28 trang 20 SBT Toán 12 Tập 1: Cho hàm số có đồ thị như hình sau:
Hãy tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
Lời giải:
Ta có: ;
.
Do đó, đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
;
.
Do đó, đường thẳng y = 1 và y = −1 là đường tiệm cận ngang của đồ thị hàm số.
Bài 1.29 trang 20 SBT Toán 12 Tập 1: Cho hàm số có đồ thị (C). Gọi tổng khoảng cách từ một điểm (x; y) ∈ (C), với x > 3, tới hai đường tiệm cận của (C) là g(x). Tìm các đường tiệm cận của đồ thị hàm số y = g(x).
Lời giải:
Đồ thị hàm số f(x) có đường tiệm cận đứng là đường thẳng x = 3 và đường tiệm cận ngang là đường thẳng y = 1.
Khoảng cách từ điểm M(x; y) ∈ (C), x > 3 đến tiệm cận đứng là d1 = x – 3.
Khoảng cách từ điểm M đến đường tiệm cận ngang là d2 = .
Vậy g(x) = d1 + d2 = x – 3 + .
Ta có: ;
Do đó đồ thị hàm số g(x) không có tiệm cận ngang
;
Do đó, đường thẳng x = 3 là đường tiệm cận đứng của đồ thị hàm số
Do đó đường thẳng y = x – 3 là đường tiệm cận xiên của đồ thị hàm số.
Bài 1.30 trang 20 SBT Toán 12 Tập 1: Một bình chứa 200 ml dung dịch muối với nồng độ 5 mg/ml.
a) Tính nồng độ dung dịch muối trong bình sau khi thêm vào x ml dung dịch muối với nồng độ 10 mg/ml.
b) Phải thêm bao nhiêu mililít vào bình để có dung dịch muối với nồng độ 9 mg/ml? Nồng độ muối trong bình có thể đạt đến 10 mg/ml được không?
Lời giải:
a) Nồng độ dung dịch muối sau khi thêm vào x ml dung dịch muối với nồng độ 10 mg/ml là: C(x) = .
b) Để dung dịch muối với nồng độ 9mg/ml, ta phải thêm vào bình x ml với x thỏa mãn
C(x) = 9 ⇔ = 9 ⇔ x = 800 (ml).
Ta có: C(x) =
C'(x) = > 0, ∀x ∈ (0; +∞).
Hàm C(x) luôn đồng biến trên khoảng (0; +∞).
Nhận thấy .
Do đó, nồng độ muối trong bình không thể đạt đến 10 mg/ml.
Lý thuyết Đường tiệm cận của đồ thị hàm số
1. Đường tiệm cận ngang
|
Đường thẳng gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu hoặc |
Ví dụ: Tìm TCN của đồ thị hàm số
Ta có:
Vậy đồ thị hàm số f(x) có TCN là y = 3.
2. Đường tiệm cận đứng
|
Đường thẳng gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:; |
Ví dụ: Tìm TCĐ của đồ thị hàm số
Ta có:
Vậy đồ thị hàm số có TCĐ là x = -2
3. Đường tiệm cận xiên
|
Đường thẳng gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu hoặc |
Ví dụ: Tìm TCX của đồ thị hàm số
Ta có:
Vậy đồ thị hàm số có TCX là y = x
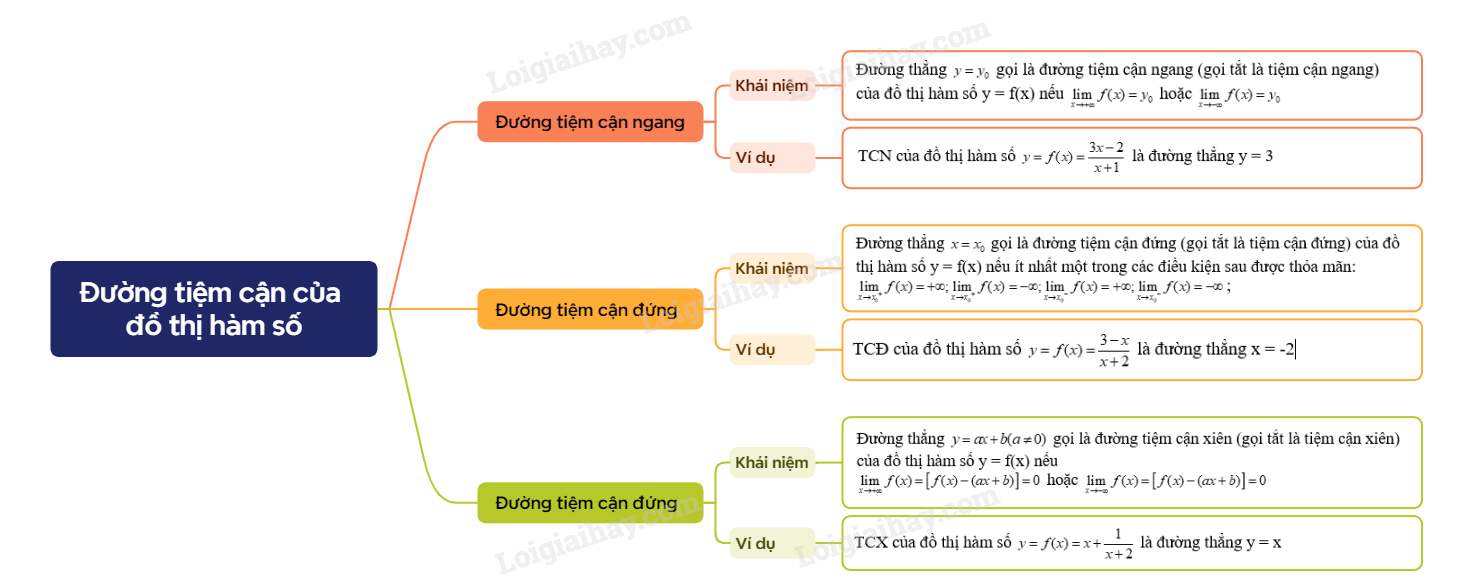
Sơ đồ tư duy Đường tiệm cận của đồ thị hàm số
Xem thêm các bài giải SBT Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 3: Đường tiệm cận của đồ thị hàm số
Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
Bài tập cuối chương 1
Bài 6: Vectơ trong không gian


