Câu 1.Hình vẽ bên là đồ thị của hàm số $y=\dfrac{ax+b}{cx+d}$. Đường tiệm cận đứng của đồ thị hàm số có phương trình là
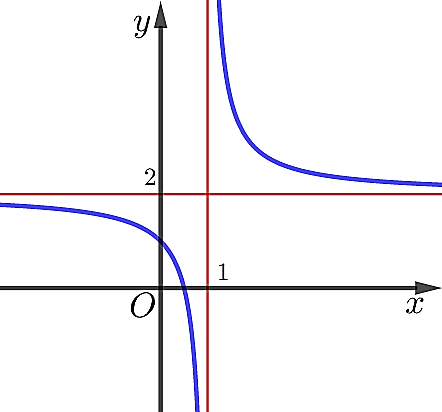
A. $x=1$.
B. $x=2$.
C. $y=1$.
D. $y=2$.
Lời giải:
Câu 2.Gọi $S$ là diện tích của hình phẳng giới hạn bởi các đường $y=5^{x}$, $y=0$, $x=0$, $x=2$. Mệnh đề nào dưới đây đúng?
A. $S=\displaystyle\int\limits_{0}^{2} 5^{x} \mathrm{\,d}x$.
B. $S=\pi \displaystyle\int\limits_{0}^{2} 5^{2x} \mathrm{\,d}x$.
C. $S=\dfrac{1}{\ln 5}\displaystyle\int\limits_{0}^{2} 5^{x} \mathrm{\,d}x$.
D. $S=\ln 5\displaystyle\int\limits_{0}^{2} 5^{x} \mathrm{\,d}x$.
Lời giải:
Diện tích hình phẳng đã cho được tính bởi công thức $S=\displaystyle\int\limits_{0}^{2} 5^{x} \mathrm{\,d}x$.
Câu 3.Giá trị lớn nhất của hàm số $f\left(x\right)=x^{3}-3x^{2}-9x+10$ trên đoạn $\left[-2\,;\,\,2\right]$ bằng
A. $-12$.
B. $10$.
C. $15$.
D. $-2$.
Lời giải:
Chọn
C.
Ta có: $f’\left(x\right)=3x^{2}-6x-9$; $f’\left(x\right)=0\Leftrightarrow 3x^{2}-6x-9=0\Leftrightarrow \left[\begin{aligned}&x=-1\,\in \left(-2\,;\,\,2\right)\\&x=3\,\notin \left(-2\,;\,\,2\right)\end{aligned}\right. $.
Ta tính được: $f\left(-2\right)=8$; $f\left(-1\right)=15$; $f\left(2\right)=-12$.
Do đó .
Câu 4.Cho hàm số$y=f\left(x\right)$có bảng xét dấu đạo hàm như sau:

Hàm số$f\left(x\right)$đồng biến trên khoảng nào sau đây?
A.$\left(0\,;\,\,1\right)$.
B.$\left(-1\,;\,\,0\right)$.
C.$\left(-\infty \,;\,\,-1\right)$.
D.$\left(-1\,;\,\,+\infty \right)$.
Lời giải:
Chọn
B.
Câu 5.Tập nghiệm của bất phương trình $3^{2x-1}>27$ là:
A. $\left(\dfrac{1}{2}\,;\,\,+\infty \right)$.
B. $\left(3\,;\,\,+\infty \right)$.
C. $\left(2\,;\,\,+\infty \right)$.
D. $\left(\dfrac{1}{3}\,;\,\,+\infty \right)$.
Lời giải:
Chọn
C.
Ta có: $3^{2x-1}>27\Leftrightarrow 3^{2x-1}>3^{3}\Leftrightarrow 2x-1>3\Leftrightarrow x>2$.
Do đó tập nghiệm phương trình là $S=\left(2\,;\,\,+\infty \right).$
Câu 6.Tìm nguyên hàm $F\left(x\right)$ của hàm số $f\left(x\right)=\sin x+\cos x$ thoả mãn $F\left(\dfrac{\pi }{2}\right)=2$.
A. $F\left(x\right)=-\cos x+\sin x+3$.
B. $F\left(x\right)=-\cos x+\sin x-1$.
C. $F\left(x\right)=-\cos x+\sin x+1$.
D. $F\left(x\right)=\cos x-\sin x+3$.
Lời giải:
Chọn
C.
Ta có: $F\left(x\right)=\displaystyle\int\limits f\left(x\right)\mathrm{\,d}x =\displaystyle\int\limits \left(\sin x+\cos x\right)\mathrm{\,d}x =-\cos x+\sin x+C$.
Mặt khác: $F\left(\dfrac{\pi }{2}\right)=-\cos \dfrac{\pi }{2}+\sin \dfrac{\pi }{2}+C=2\Rightarrow 1+C=2\Rightarrow C=1$.
Câu 7.Cho cấp số cộng $\left(u_{n}\right)$ với năm số hạng đầu là $2;\,\,7;\,\,12;\,\,17;\,\,22$. Số hạng tổng quát của cấp số cộng là
A. $u_{n}=3n+5$.
B. $u_{n}=3n-5$.
C. $u_{n}=5n+3$.
D. $u_{n}=5n-3$.
Lời giải:
Chọn
D.
Cấp số cộng $\left(u_{n}\right)$ có số hạng đầu $u_{1}=2$ và công sai $d=5$.
Số hạng tổng quát của $\left(u_{n}\right)$ là: $u_{n}=u_{1}+\left(n-1\right)d$ hay $u_{n}=2+\left(n-1\right)5=5n-3$.
Câu 8.Bảng dưới đây thống kê cự li ném tạ trong quá trình luyện tập của một vận động viên trong một tuần (đơn vị: mét).

Hãy tính phương sai của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần nghìn).
A. $0,277$.
B. $0,526$.
C. $0,326$.
D. $0,211$.
Lời giải:
Ta viết lại bảng có bổ sung hàng cho giá trị đại diện:

Cỡ mẫu là n = 13 + 45 + 24 + 12 + 6 = 100.
Số trung bình của mẫu số liệu ghép nhóm là:
$\bar x=\dfrac{13\cdot 19,25+45\cdot 19,75+24\cdot 20,25+12\cdot 20,75+6\cdot 21,25}{100}=20,015$.
Phương sai của mẫu số liệu ghép nhóm là:
$s^{2}=\dfrac{13\cdot (19,25-\bar x)^{2}+45\cdot (19,75-\bar x)^{2}+24\cdot (20,25-\bar x)+12\cdot (20,75-\bar x)^{2}+6\cdot (21,25-\bar x)^{2}}{100}\approx 0,277$.
Câu 9.Cho hai mặt phẳng $\left(P\right):2x-y-z-3=0$ và $\left(Q\right):x-z-2=0$. Góc giữa hai mặt phẳng $\left(P\right)$ và $\left(Q\right)$ bằng
A. $30^{\circ }$.
B. $45^{\circ }$.
C. $60^{\circ }$.
D. $90^{\circ }$.
Lời giải:
Véctơ pháp tuyến của mặt phẳng $\left(P\right)$ và $\left(Q\right)$ lần lượt là $\vec n_{1}=\left(2\,;\,\,-1\,;\,\,-1\right)\,;\,\,\vec n_{2}=\left(1\,;\,\,0\,;\,\,-1\right)$
Ta có: $\cos \left(\left(P\right)\,,\,\,\left(Q\right)\right)=\dfrac{\left|{\vec n}_{1}.{\vec n}_{2}\right|}{\left|{\vec n}_{1}\right|\left|{\vec n}_{2}\right|}=\dfrac{\sqrt {3} }{2}\Rightarrow \left(\left(P\right)\,,\,\,\left(Q\right)\right)=30^{\circ }$.
Câu 10.Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Mốt của mẫu số liệu ghép nhóm trên là
A. $52$.
B. $42$.
C. $53$.
D.$54$.
Lời giải:
Nhóm chứa mốt (nhóm có tần số cao nhất) là $[40\,;\,\,60)$.
Ta có: $u_{m}=40\,;\,\,u_{m+1}=60\Rightarrow u_{m+1}-u_{m}=60-40=20$; $n_{m-1}=9\,;\,\,n_{m}=12\,;\,\,n_{m+1}=10$.
Mốt của mẫu số liệu ghép nhóm là $M_{0}=40+\dfrac{12-9}{\begin{array}{*{20}{l}}(12-9)\mathrm{\, }+\mathrm{\, }(1\end{array}2-10)}\cdot 20=52$.
Câu 11.Một vật chuyển động có phương trình $s\left(t\right)=3\cos t$. Khi đó, vận tốc tức thời tại thời điểm $t$ của vật là:
A. $v\left(t\right)=-3\sin t$.
B. $v\left(t\right)=-3\cos t$.
C. $v\left(t\right)=3\cos t$.
D. $v\left(t\right)=3\sin t.$
Lời giải:
Ta có: $v\left(t\right)=s’\left(t\right)=\left(3\cos t\right)^{\prime }=-3\sin t$.
Câu 12.Trong không gian $Oxyz$, một vectơ pháp tuyến của mặt phẳng $\dfrac{x}{-2}+\dfrac{y}{-1}+\dfrac{z}{3}=1$ là
A. $\vec n=(3\,;\,\,6\,;\,\,-2)$.
B. $\vec n=(2\,;\,\,-1\,;\,\,3)$.
C. $\vec n=(-3\,;\,\,-6\,;\,\,-2)$.
D. $\overrightarrow {n} =(-2\,;\,\,-1\,;\,\,3)$.
Lời giải:
Phương trình $\dfrac{x}{-2}+\dfrac{y}{-1}+\dfrac{z}{3}=1\Leftrightarrow 3x+6y-2z+6=0.$
Mặt phẳng có một vectơ pháp tuyến là $\vec n=(3\,;\,\,6\,;\,\,-2)$.
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Câu 13.Cho hàm số $y=f\left(x\right)=\dfrac{x-m^{2}+m}{x+1}$, m là tham số.
a) Với $m=1$ thì hàm số $y=f\left(x\right)$ luôn nghịch biến trên các khoảng $\left(-\infty \,;\,\,-1\right)$ và $\left(-1\,;\,\,+\infty \right)$.
b) Với mọi số thực m thì hàm số $y=f\left(x\right)$ luôn đồng biến trên các khoảng $\left(-\infty \,;\,\,-1\right)$ và $\left(-1\,;\,\,+\infty \right)$.
c) $\max \limits_{\left[1\,\,;\,\,2\right]} f\left(x\right)=f\left(2\right)$.
d) Có hai giá trị nguyên m để $\min \limits_{\left[0\,;\,\,1\right]} f\left(x\right)=-2$.
Lời giải:
a) Mệnh đề sai.
Tập xác định hàm số: $D=\mathbb{R}\backslash \left\{-1\right\}$.
Với $m=1$ thì $f\left(x\right)=\dfrac{x}{x+1}\,;$$f’\left(x\right)=\dfrac{1}{\left(x+1\right)^{2}}>0\,,\,\,\forall x\neq -1$.
Hàm số đồng biến trên từng khoảng xác định của nó.
b) Mệnh đề đúng.
Ta có $f’\left(x\right)=\dfrac{m^{2}-m+1}{\left(x+1\right)^{2}}>0\,,\,\,\forall m\in \mathbb{R}\,,\,\,\forall x\neq -1$. Do đó hàm số luôn đồng biến trên từng khoảng xác định của nó.
c) Mệnh đề đúng.
Vì $y=f\left(x\right)$ luôn đồng biến trên từng khoảng xác định của nó nên ta có:
$1\leq x\leq 2\Rightarrow f\left(1\right)\leq f\left(x\right)\leq f\left(2\right)$.
Do đó: $\max \limits_{\left[1\,\,;\,\,2\right]} f\left(x\right)=f\left(2\right)$.
d) Mệnh đề đúng.
Vì $y=f\left(x\right)$ luôn đồng biến trên từng khoảng xác định của nó nên ta có:
$0\leq x\leq 1\Rightarrow f\left(0\right)\leq f\left(x\right)\leq f\left(1\right)$.
Khi đó $\min \limits_{\left[0\,;\,\,1\right]} f\left(x\right)=-2\Leftrightarrow f\left(0\right)=2\Leftrightarrow \dfrac{-m^{2}+m}{1}=-2\Leftrightarrow \left[\begin{aligned}&m=2\\&m=-1\end{aligned}\right. $.
Vậy có hai giá trị nguyên của m thỏa mãn $\min \limits_{\left[0\,;\,\,1\right]} f\left(x\right)=-2$.
Câu 14.

Một vật chuyển động trong $3$ giờ với vận tốc $v$ (km/h) phụ thuộc vào thời gian $t$ (h), đồ thị của hàm vận tốc được cho như hình vẽ. Trong thời gian $1$ giờ kể từ khi vật bắt đầu chuyển động, đồ thị hàm vận tốc của nó là một phần của parabol có đỉnh $S(2\,;\,\,9)$, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành.
a) Tại thời điểm bắt đầu chuyển động, vật có vận tốc bằng $4$ km/h.
b) Trong thời gian $1$ giờ kể từ khi bắt đầu chuyển động, phương trình vận tốc của vật là $v(t)=-\dfrac{5}{4}t^{2}-5t+4.$
c) Sau $30$ phút kể từ khi bắt đầu chuyển động, gia tốc của vật bằng $3,75$ km/h2.
d) Quãng đường $S$ mà vật đi được được trong $3$ giờ (làm tròn đến hàng phần trăm) là $21,58$km.
Lời giải:
a) Mệnh đề đúng.
Với $t=0$ thì $v=4$ km/h (xem đồ thị hàm vận tốc).
b) Mệnh đề sai.
Gọi hàm vận tốc của vật trong 1 giờ đầu tiên là $v(t)=at^{2}+bt+c$ $(a\neq 0).$
Vì đồ thị hàm số $y=v\left(t\right)$ đi qua các điểm $\left(0\,;\,\,4\right)\,,\,\,\left(2\,;\,\,9\right)$ và hàm số đạt cực đại tại $x=2$ nên ta có hệ phương trình:
Ta có $\left\{\begin{aligned}&c=4\\&4a+2b+c=9\\&-\dfrac{b}{2a}=2\end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&c=4\\&4a+2b+c=9\\&4a+b=0\end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&a=-\dfrac{5}{4}\\&b=5\\&c=4\end{aligned}\right. .$
Vậy
c) Mệnh đề đúng.
Với $t\in [0\,;\,\,1]$ thì gia tốc của vật là $a(t)=v'(t)=-\dfrac{5}{2}t+5.$
Do đó $a(0,5)=-\dfrac{5}{2}.0,5+5=3,75$km/h2.
d) Mệnh đề đúng.
Ta có $v(1)=\dfrac{31}{4},$ hàm vận tốc của vật với $t\in \left(1\,;\,\,3\right]$ là $v(t)=\dfrac{31}{4}.$
Do đó ta được $v(t)=\left\{\begin{aligned}&-\dfrac{5}{4}t^{2}+5t+4\mathrm{\, khi }0\leq t\leq 1\\&\dfrac{31}{4}\mathrm{\, } & \mathrm{\,khi }1<t\leq 3\end{aligned}\right. .$
Quãng đường $S$ mà vật di chuyển được trong $3$ giờ là:
Câu 15.Trong một căn phòng có chiều ngang 4 m, chiều rộng 8 m và chiều cao 4 m, người chủ đã thiết kế 4 dãy đèn led chạy dọc theo các đường chéo của hình chữ nhật tương ứng với các bức tường căn phòng sao cho chúng có tính liên tục. Thiết lập hệ trục tọa độ Oxyz như hình vẽ với căn phòng là hình hộp chữ nhật $ABCD.A’B’C’D’$, trong đó điểm A là gốc tọa độ, đơn vị trên mỗi trục là mét.
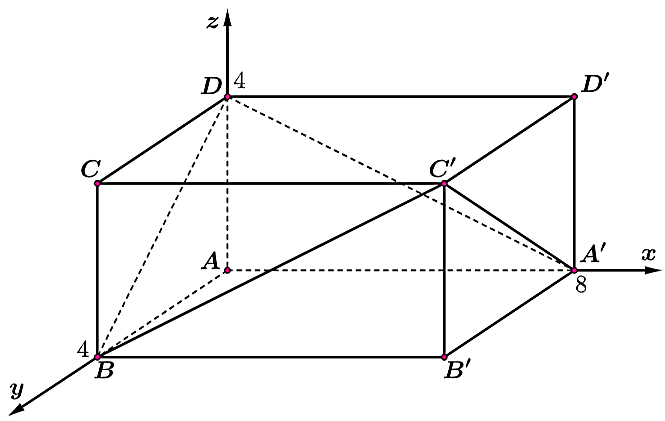

Chủ căn phòng quyết định sử dụng loại đèn LED neon Flex (không chói mắt) với giá thị trường khoảng 85 nghìn đồng/mét.
a) Phương trình cạnh BD là $\left\{\begin{aligned}&x=0\\&y=4+t\\&z=t\end{aligned}\right. $ (t là tham số).
b) Số tiền để mua đèn led trang trí trong căn phòng là $2\,482$(nghìn đồng), làm tròn đến hàng đơn vị của nghìn đồng.
c) Khoảng cách từ D đến mặt phẳng $\left(A’BC’\right)$ bằng $5,2\,\,m$ (làm tròn đến hàng phần chục).
d) Biết đèn LED có điểm sáng M chạy từ B đến D với tốc độ $0,2$ m/s , đèn LED có điểm sáng N chạy từ $A’$ đến $C’$ với tốc độ $0,3$ m/s. Sau 9,1 giây (làm tròn đến hàng phần chục) kể từ khi mở nguồn thì hai điểm sáng M, N có khoảng cách ngắn nhất trước khi có ít nhất một điểm sáng về đích.
Lời giải:
Tọa độ các điểm $A\left(0\,;\,\,0;\,\,0\right)\,,\,\,A’\left(8\,;\,\,0\,;\,\,0\right)\,,\,\,B\left(0\,;\,\,4\,;\,\,0\right)\,,\,\,D\left(0\,;\,\,0\,;\,\,4\right)\,,\,\,C’\left(8\,;\,\,4\,;\,\,4\right)$.
a) Mệnh đề sai.
BD qua $B\left(0\,;\,\,4\,;\,\,0\right)$ và có vectơ chỉ phương $\overrightarrow {BD} =\left(0\,;\,\,4\,;\,\,-4\right)=4\left(0\,;\,\,1\,;\,\,-1\right)$ nên có phương trình chính tắc là $\left\{\begin{aligned}&x=0\\&y=4+t\\&z=-t\end{aligned}\right. $.
b) Mệnh đề đúng.
Ta có $BD=A’C’=4\sqrt {2} \,;\,\,BC’=A’D=\sqrt {4^{2}+8^{2}} =4\sqrt {5} $.
Số tiền để mua đèn led cho căn phòng là $2\left(4\sqrt {2} +4\sqrt {5} \right) \times 85\approx 2\,482$ (nghìn đồng).
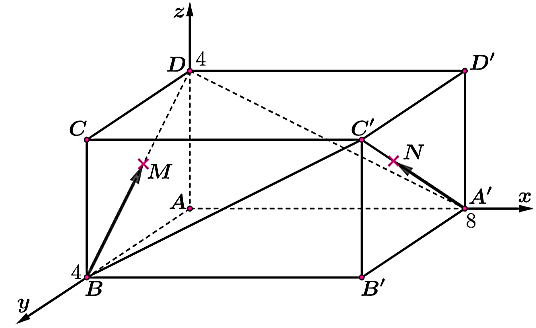
c) Mệnh đề sai.
Ta có: $\overrightarrow {BA’} =\left(8\,;\,\,-4\,;\,\,0\right)\,,\,\,\overrightarrow {BC’} =\left(8\,;\,\,0\,;\,\,4\right)$$\Rightarrow \left[\overrightarrow {BA’} \,,\,\,\overrightarrow {BC’} \right]=\left(-16\,;\,\,-32\,;\,\,32\right)=-16\left(1\,;\,\,2\,;\,\,-2\right)$.
Mặt phẳng $\left(A’BC’\right)$ qua $B\left(0\,;\,\,4\,;\,\,0\right)$, có một vectơ pháp tuyến $\vec n=\left(1\,;\,\,2\,;\,\,-2\right)$ nên có phương trình tổng quát .
Khoảng cách cần tính: $d\left(O\,,\,\,\left(A’BC’\right)\right)=\dfrac{\left|-2\cdot 4-8\right|}{\sqrt {1^{2}+2^{2}+\left(-2\right)^{2}} }=\dfrac{16}{3}\approx 5,3\,\,m$.
d) Mệnh đề sai.
Ta có $\overrightarrow {BD} =\left(0\,;\,\,-4\,;\,\,4\right)\Rightarrow \vec u=0,2 \times \dfrac{1}{BD}\overrightarrow {BD} =\left(0\,;\,\,-\dfrac{\sqrt {2} }{10}\,;\,\,\dfrac{\sqrt {2} }{10}\right)$ là vectơ chỉ phương của BD.
Điểm $M\in BD$ nên tại thời điểm t, điểm M ở vị trí .
Ta có $\overrightarrow {A’C’} =\left(0\,;\,\,4\,;\,\,4\right)\Rightarrow \vec v=0,3 \times \dfrac{1}{A’C’}\overrightarrow {A’C’} =\left(0\,;\,\,\dfrac{3\sqrt {2} }{20}\,;\,\,\dfrac{3\sqrt {2} }{20}\right)$ là vectơ chỉ phương của $A’C’$. Điểm $N\in A’C’$ nên tại thời điểm t, điểm N ở vị trí .
Do đó $\overrightarrow {MN} =\left(8\,;\,\,\dfrac{\sqrt {2} }{4}t-4\,;\,\,\dfrac{\sqrt {2} }{20}t\right)\Rightarrow MN^{2}=8^{2}+\left(\dfrac{\sqrt {2} }{4}t-4\right)^{2}+\left(\dfrac{\sqrt {2} }{20}t\right)^{2}=\dfrac{13}{100}t^{2}-2\sqrt {2} t+80$.
Dễ thấy $MN=\sqrt {\dfrac{13}{100}t^{2}-2\sqrt {2} t+80} $ đạt giá trị nhỏ nhất $MN_{\min }\approx 8,04$; khi đó giây.
Câu 16.Hộp I đựng 3 bi xanh và 2 bi vàng; hộp II có 3 bi xanh, 1 bi đen và 1 bi vàng; hộp III có 1 bi xanh, 1 bi đen và 3 bi vàng. Lấy ngẫu nhiên 1 viên bi từ hộp I bỏ sang hộp II; đồng thời lấy ngẫu nhiên 1 viên bi từ hộp III bỏ sang hộp II; sau đó lấy ngẫu nhiên 2 viên bi từ hộp II.
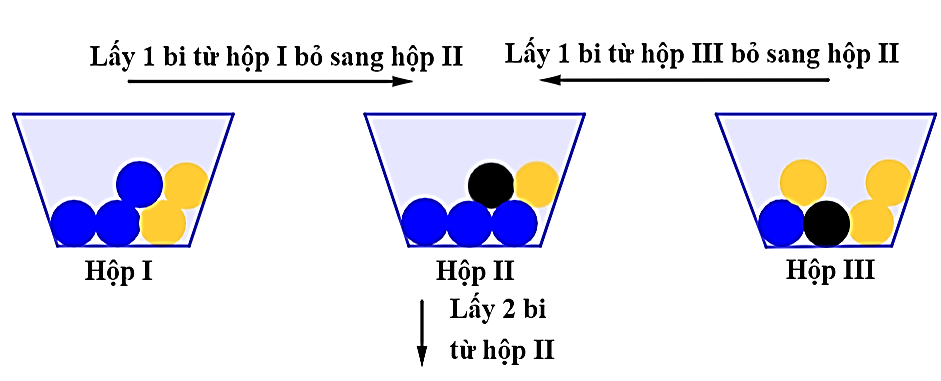
a) Xác suất để hộp thứ II nhận được 2 bi cùng màu bằng $\dfrac{8}{25}$.
b) Xác suất để lấy được 2 bi đen từ hộp II bằng $\dfrac{1}{105}$.
c) Xác suất để lấy được 2 bi vàng từ hộp II bằng $\dfrac{31}{525}$.
d) Xác suất để lấy được 2 bi từ hộp II cũng là 2 bi được chuyển sang từ hai hộp I, III bằng $\dfrac{5}{31}$, biết rằng đó là 2 viên bi vàng.
Lời giải:
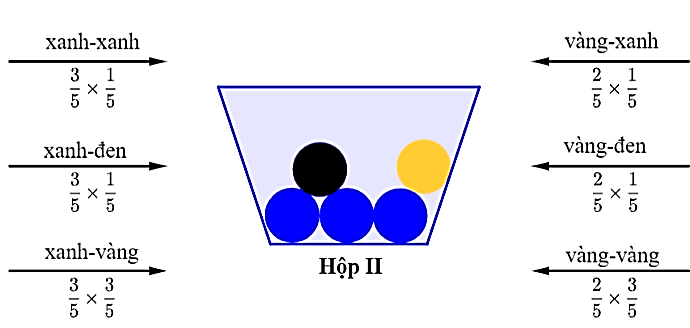
a) Mệnh đề sai.
Xác suất để hộp II nhận được 2 bi cùng màu bằng .
(Vì theo sơ đồ, ta chỉ xét hai trường hợp xanh-xanh hoặc vàng-vàng).
b) Mệnh đề đúng.
Trường hợp lấy được từ hộp II 2 bi đen chỉ xảy ra nếu trước đó hộp II đã nhận cặp bi xanh-đen hoặc vàng-đen từ hai hộp I, III.
Do vậy xác suất để lấy được 2 bi đen từ hộp II bằng .
c) Mệnh đề đúng.
Gọi A là biến cố: "Lấy được 2 bi vàng từ hộp II".
Lưu ý rằng: Muốn hộp II có đủ bi vàng để lấy ra 2 bi thì trước đó nó phải nhận 1 đến 2 bi vàng từ hai hộp I và III.
Ta có: .
d) Mệnh đề sai.
Gọi B là biến cố: "Lấy được 2 bi từ hộp II cũng là 2 bi được chuyển sang từ hai hộp I, III".
Ta có: .
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 17.Một người đưa thư xuất phát từ bưu điện (vị trí A) và phải đi qua các con đường để phát thư trước khi quay trở lại bưu điện. Sơ đồ các con đường cần đi qua và độ dài của chúng (tính theo mét) được biểu diễn ở hình vẽ dưới. Hỏi người đó phải đi như thế nào để đường đi là ngắn nhất?
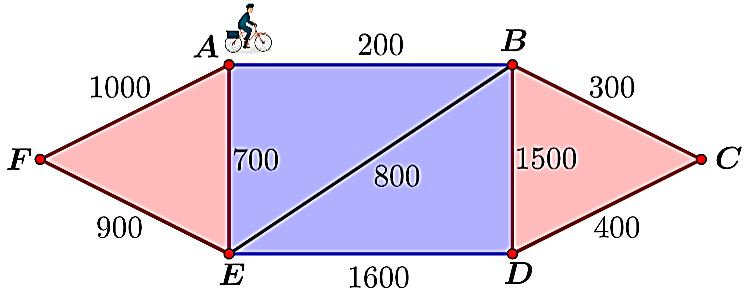
Đáp số: 8300
Lời giải:
Đồ thị trên chỉ có hai đỉnh bậc lẻ là A và D nên ta có thể tìm được một đường đi Euler từ A đến D (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ A đến D là AFEABEDBCD và tổng độ dài của nó là
1000 + 900 + 700 + 200 + 800 + 1600 + 1500 + 300 + 400 = 7400.
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ D đến A theo thuật toán gắn nhãn vĩnh viễn.
Đường đi ngắn nhất từ D đến A là DCBA và có độ dài là 400 + 300 + 200 = 900.
Vậy một chu trình cần tìm là AFEABEDBCDCBA và có độ dài là 7400 + 900 = 8300.
Câu 18.Cho đồ thị hàm số $y=\sqrt {x^{2}-4x+3} $ có các đường tiệm cận xiên $d_{1}$ và $d_{2}$. Tìm tổng khoảng cách từ gốc tọa độ đến hai đường tiệm cận xiên $d_{1}\,,\,\,d_{2}$ (kết quả được làm tròn đến hàng phần trăm).
Đáp số: 2,83
Lời giải:
Điều kiện xác định hàm số là $x^{2}-4x+3\geq 0\Leftrightarrow \left[\begin{aligned}&x\leq 1\\&x\geq 3\end{aligned}\right. $.
Xét
$=\lim \limits_{x\to +\infty } \dfrac{-4x+3}{\sqrt {x^{2}-4x+3} +x}$.
Do đó $d_{1}:y=x-2\,\,\mathrm{\,hay}\,\,d_{1}:x-y-2=0$ là một đường tiệm cận xiên của đồ thị hàm số.
Xét
$=\lim \limits_{x\to -\infty } \dfrac{-4x+3}{\sqrt {x^{2}-4x+3} -x}$.
Do đó $d_{2}:y=-x+2\,\,\mathrm{\,hay}\,\,d_{2}:x+y-2=0$ là một đường tiệm cận xiên của đồ thị hàm số.
Ta có: .
Câu 19.

Một chiếc bánh kem mừng sinh nhật có dạng hình chóp cụt đều $ABC.A’B’C’$ với cạnh đáy lớn bằng $4\,\,dm$, cạnh đáy nhỏ bằng $2\,\,\,dm$ và chiều cao của nó bằng $1,5\,\,dm$. Tìm thể tích của chiếc bánh kem đó theo đơn vị $dm^{3}$(làm tròn đến hàng phần trăm, bỏ qua những thứ trang trí quanh chiếc bánh).
Đáp số: 6,06
Lời giải:
Xét hình chóp cụt đều $ABC.A’B’C’$ như hình vẽ; trong đó chiều cao $h=IO=1,5\,\,dm$.
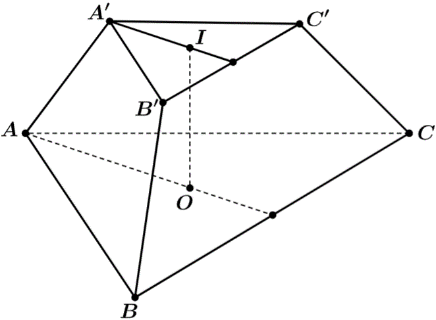
Diện tích hai đáy hình chóp cụt đều: $S_{1}=S_{\Delta ABC}=\dfrac{4^{2}\sqrt {3} }{4}=4\sqrt {3} \,\,dm^{2}$; $S_{2}=S_{\Delta A’B’C’}=\dfrac{2^{2}\sqrt {3} }{4}=\sqrt {3} \,\,dm^{2}$.
Thể tích khối chóp cụt đều: $V=\dfrac{1}{3}h\left(S_{1}+\sqrt {S_{1}S_{2}} +S_{2}\right)$.
Câu 20.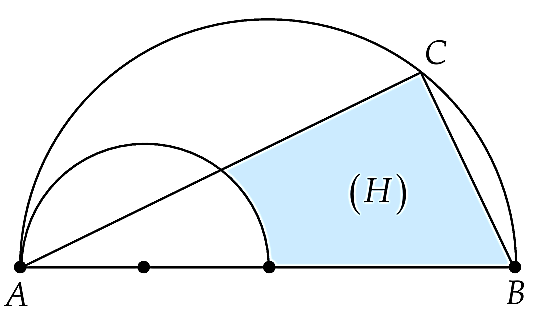
Cho hai nửa đường tròn như hình vẽ bên, trong đó đường kính của nửa đường tròn lớn gấp đôi đường kính của nửa đường tròn nhỏ. Biết rằng nửa hình tròn đường kính AB có diện tích $8\pi $ và $\widehat {ABC}=60^{\circ }$.
Tính thể tích vật thể tròn xoay tạo thành khi quay hình phẳng (H) (phần được tô đậm) quanh đường thẳng AB? Kết quả được làm tròn đến hàng phần trăm.
Đáp số: 85,9
Lời giải:
Diện tích nửa đường tròn đường kính AB là $\dfrac{1}{2}\cdot \pi \left(\dfrac{AB}{2}\right)^{2}=8\pi \Rightarrow AB=8$.
Xét hệ trục tọa độ Oxy như hình vẽ với $O\equiv A$ và tia AB trùng với tia Ox.

Đường thẳng AC có phương trình là d:$y=\dfrac{\sqrt {3} }{3}x$ (vì AC đi qua $A\left(0\,;\,\,0\right)$ và có hệ số góc $k=\tan \widehat {BAC}=\tan 30^{\circ }=\dfrac{\sqrt {3} }{3}$).
Gọi $\left(C\right)$ là đường tròn tâm $\left(2\,;\,\,0\right)$, bán kính $R=2$; khi đó phương trình $\left(C\right):\left(x-2\right)^{2}+y^{2}=4$.
Hoành độ giao điểm giữa d và đường tròn $\left(C\right)$ thỏa mãn phương trình $\left(x-2\right)^{2}+\left(\dfrac{\sqrt {3} }{3}x\right)^{2}=4\Leftrightarrow \dfrac{4}{3}x^{2}-4x=0\Leftrightarrow \left[\begin{aligned}&x=0\\&x=3\end{aligned}\right. $.
Đường thẳng BC qua $B\left(8\,;\,\,0\right)$, vuông góc d:$y=\dfrac{\sqrt {3} }{3}x$ nên có phương trình $y=-\sqrt {3} \left(x-8\right)$.
Hai đường thẳng AC, BC cắt nhau tại C thỏa hệ $\left\{\begin{aligned}&y=\dfrac{\sqrt {3} }{3}x\\&y=-\sqrt {3} \left(x-8\right)\end{aligned}\right. \Rightarrow C\left(6\,;\,\,2\sqrt {3} \right)$.
Thể tích khối tròn xoay khi quay tam giác ABC quanh Ox là .
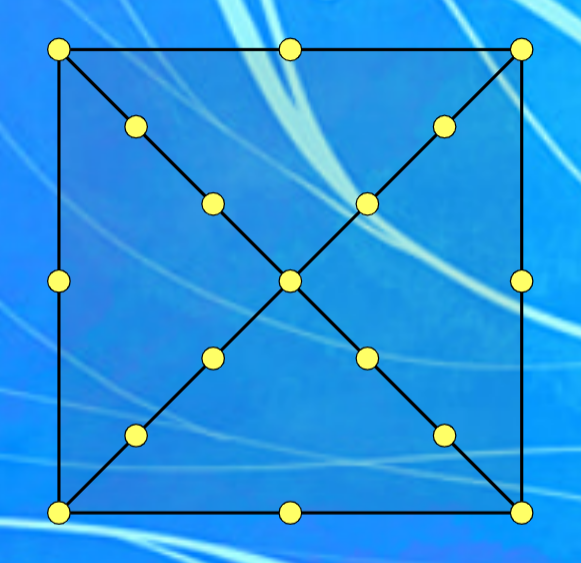
Câu 21.Trên một banner quảng cáo, người ta gắn 17 chiếc bóng đèn vào một khung hình vuông cũng như hai đường chéo của hình vuông đó. Biết rằng các bóng đèn trên một cạnh hoặc đường chéo thì chia cạnh hoặc đường chéo đó làm các đoạn bằng nhau (xem hình vẽ). Các bóng đèn sẽ sáng lên theo quy luật sau:
Vào phút thứ nhất sẽ có ngẫu nhiên 1 bóng đèn sáng lên, đến cuối phút thứ nhất nó sẽ tắt.
Vào phút thứ 2 sẽ có ngẫu nhiên 2 bóng đèn sáng lên, đến cuối phút thứ hai chúng sẽ tắt.
Vào phút thứ 3 sẽ có ngẫu nhiên 3 bóng đèn sáng lên, đến cuối phút thứ ba chúng sẽ tắt.
Quy luật này cứ tiếp diễn cho đến phút thứ 17 và một chu trình mới sẽ được lặp lại. Tính xác suất để từ phút thứ 3 cho đến phút thứ 17, luôn có ít nhất 3 bóng đèn sáng lên ở 3 đỉnh của một tam giác (làm tròn đến hàng phần trăm).
Đáp số: 0,84
Lời giải:
Gọi $A_{i}$ là biến cố: "Tại phút thứ i thì có ít nhất 3 bóng đèn sáng lên ở 3 đỉnh của tam giác"; khi đó $i\in \left\{3\,;\,\,4\,;\,…\,;\,\,17\right\}$.
Phút thứ 3:
Số phần tử không gian mẫu là $n\left(\Omega _{3}\right)=C_{17}^{3}$.
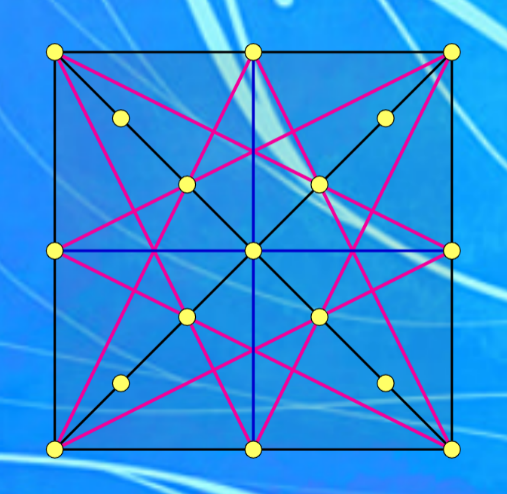
Số khả năng để 3 bóng đèn sáng lên là 3 đỉnh tam giác: $n\left(A_{3}\right)=C_{17}^{3}-2C_{7}^{3}-4-10=596$.
(Ta loại trừ các trường hợp 3 điểm thẳng hàng gồm: 2 trường hợp 3 điểm thuộc các đường chéo, 4 trường hợp 3 điểm thuộc các cạnh, 10 trường hợp 3 điểm thẳng hàng khi vẽ thêm hình).
Xác suất tương ứng là $P\left(A_{3}\right)=\dfrac{n\left(A_{3}\right)}{n\left(\Omega _{3}\right)}=\dfrac{598}{C_{17}^{3}}=\dfrac{299}{340}$.
Phút thứ 4: Xác suất tương ứng là $P\left(A_{4}\right)=\dfrac{C_{17}^{4}-2C_{7}^{4}}{C_{17}^{4}}=\dfrac{33}{34}$.
Phút thứ 5: Xác suất tương ứng là $P\left(A_{5}\right)=\dfrac{C_{17}^{5}-2C_{7}^{5}}{C_{17}^{5}}=\dfrac{439}{442}$.
Phút thứ 6: Xác suất tương ứng là $P\left(A_{6}\right)=\dfrac{C_{17}^{6}-2C_{7}^{6}}{C_{17}^{6}}=\dfrac{883}{884}$.
Phút thứ 7: Xác suất tương ứng là $P\left(A_{7}\right)=\dfrac{C_{17}^{7}-2}{C_{17}^{7}}=\dfrac{9\,723}{9\,724}$.
Từ phút thứ 8 trở đi thì chắc chắn luôn có ít nhất 3 bóng sáng lên ở 3 đỉnh của tam giác.
Xác suất cần tìm là .
Câu 22.Trong không gian với hệ trục tọa độ $Oxyz,$ cho ba điểm $A\left(3\,;0\,;0\right),B\left(-3\,;0\,;0\right)$ và $C\left(0\,;5\,;1\right)$. Gọi $M$ là một điểm nằm trên mặt phẳng tọa độ $\left(Oxy\right)$ sao cho $MA+MB=10,$ giá trị nhỏ nhất của $MC$ bằng bao nhiêu (làm tròn đến hàng phần trăm).
Đáp số: 1,41
Lời giải:
🖎 Nhận xét: Hai điểm $A,\,\,B$ cùng thuộc mặt phẳng $\left(Oxy\right)$ và $MA+MB=10>6=AB$. Do vậy, tập hợp điểm M là một elip thuộc mặt phẳng $\left(Oxy\right)$ với hai tiểu điểm là A và
B.
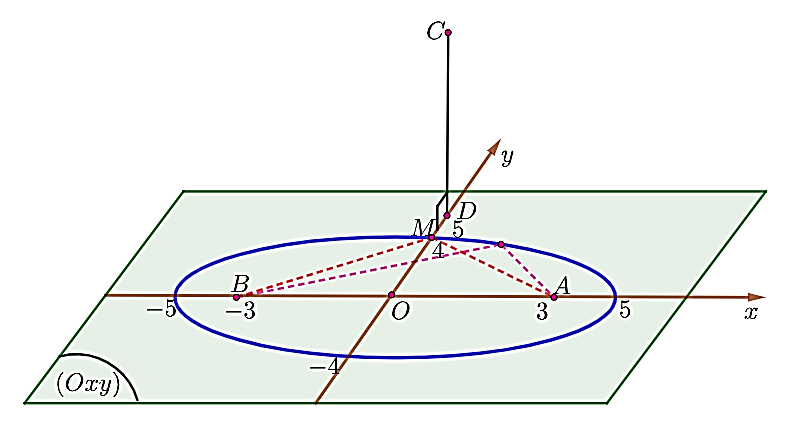
Đặt $MA+MB=2a=10\Rightarrow a=5$, $AB=2c=6\Rightarrow c=3$, $b=\sqrt {a^{2}-c^{2}} =\sqrt {5^{2}-3^{2}} =4$.
Do vậy $M\in \left(E\right):\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ hay $M\in \left(E\right):\dfrac{x^{2}}{25}+\dfrac{y^{2}}{16}=1$.
Gọi $D\left(0;5;0\right)$là hình chiếu của $C$ trên mặt phẳng $\left(Oxy\right)$. Khi đó ta có: $CD=\sqrt {0^{2}+0^{2}+1^{2}} =1$ và
$MC=\sqrt {CD^{2}+DM^{2}} =\sqrt {1+DM^{2}} \,\,\,\,\left(*\right)$. Do vậy$MC$ bé nhất khi và chỉ khi $DM$ bé nhất.
Theo hình vẽ, ta thấy khi M trùng với đỉnh elip (E) thuộc tia Oy thì $DM$ bé nhất, hay $M\left(0;4;0\right)$.
Suy ra $DM=1$, khi đó .